 por leticiapires52 » Sex Mai 30, 2014 13:06
por leticiapires52 » Sex Mai 30, 2014 13:06
Maria, Mariana e Mariam são irmâs, elas têm atualmente idades que estão em uma PA de razão 4. Daqui a cinco anos, suas idades:
a) Estarão em uma PA de razão 5.
b) Estarão em uma PA de razão 4.
c) Estarão em uma PA de razão 2.
d) Estarão em uma PA de razão 6.
e) Estarão em uma PA de razão 3.
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Ter Jun 03, 2014 21:10
por DanielFerreira » Ter Jun 03, 2014 21:10
Leticia, daqui a cinco anos a idade das três irmãs continuará com uma diferença de 4 anos, veja:
Supomos que Maria seja a mais velha, Mariana a do meio e Mariam a caçula, então suas idades são:
Mariam: x
Mariana: x + 4
Maria: (x + 4) + 4
Daqui a cinco anos,
Mariam: x ==============> x + 5 ============> x + 5
Mariana: x + 4 ==========> (x + 4) + 5 ========> x + 9
Maria: (x + 4) + 4 =======> [(x + 4) + 4] + 5 ===> x + 13
Verifique!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por leticiapires52 » Ter Jun 03, 2014 21:24
por leticiapires52 » Ter Jun 03, 2014 21:24
eu também achei 4, mas fazendo de outro jeito, não sei se fiz certo
an = a1 + ( n - 1) .r
a5= 4 + ( 3 - 1). 4
a5= 4 + (2). 4
a5= 4 + 8
a5= 12
r = a5 - a4
4 = 12 - a4
4 - 12 = -a4
-8= - a4
a4 = 8
r = 12 -8
r=4
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Ter Jun 03, 2014 21:30
por DanielFerreira » Ter Jun 03, 2014 21:30
Letícia,
pelos dados do enunciado, não se pode precisar as idades. Como sabe que
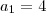
? E o

?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por leticiapires52 » Ter Jun 03, 2014 21:43
por leticiapires52 » Ter Jun 03, 2014 21:43
usei n = 3 pke são 3 irmãs, e o a1 fui pela razão
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- RAZÃO
por hevhoram » Qua Jun 02, 2010 11:50
- 1 Respostas
- 1535 Exibições
- Última mensagem por Molina

Qua Jun 02, 2010 18:43
Álgebra Elementar
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1680 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2408 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
-
- razão
por angeloka » Sex Out 15, 2010 19:29
- 8 Respostas
- 6800 Exibições
- Última mensagem por MarceloFantini

Sáb Out 23, 2010 01:41
Álgebra Elementar
-
- PA com razão 0,3
por gustavowelp » Sex Nov 19, 2010 08:42
- 5 Respostas
- 3448 Exibições
- Última mensagem por 0 kelvin

Sex Nov 19, 2010 15:51
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



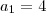 ? E o
? E o  ?
?

 , avisa que eu resolvo.
, avisa que eu resolvo.

