 por Thais Camerino » Dom Mai 25, 2014 20:51
por Thais Camerino » Dom Mai 25, 2014 20:51
Olá!
Queria pedir ajuda para o raciocínio deste tipo d equação.
Eu já vi que neste caso tem q se colocar o 3^x^-1 em evidencia.. mas não percebo, e este tipo de questão já vi varias vezes mas não sei pq é feito desta maneira..
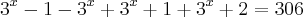
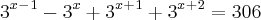
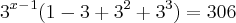
(Porque tem aquele 1 dentro dos parênteses? como ficou assim?)
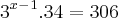
(Porque 34? )
Se alguêm pudesse explicar-me, ficaria grata! (:
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Dom Mai 25, 2014 21:34
por e8group » Dom Mai 25, 2014 21:34
Você quer dizer
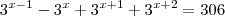
? Se sim , note que podemos multiplicar a eq. por 1, vejamos que
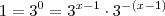
e
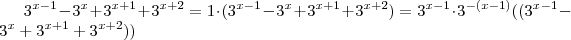
que devido propriedade associativa
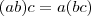
+ a distributiva
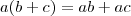
, resulta
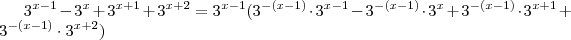
.
Dentro do parêntesis , você conserva a base e soma os expoentes e obtêm aquilo que você postou , e somando estes termos obterá 34 .
Entendeu ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Seg Mai 26, 2014 15:33
por Thais Camerino » Seg Mai 26, 2014 15:33
santhiago escreveu:Você quer dizer
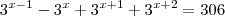
? Se sim , note que podemos multiplicar a eq. por 1, vejamos que
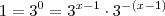
e
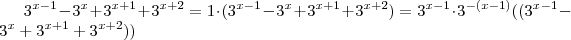
que devido propriedade associativa
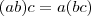
+ a distributiva
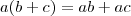
, resulta
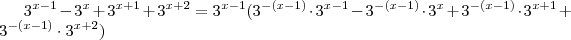
.
Dentro do parêntesis , você conserva a base e soma os expoentes e obtêm aquilo que você postou , e somando estes termos obterá 34 .
Entendeu ?
É sim! Hum, eu entendi individualmente mas não como um todo :s
Principalmente a transição da primeira parte para a segunda.. tentei fazer na conta q vc postou, fazendo a distributiva nos expoentes mas saiu uma coisa absurda. Não tou sabendo fazer
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Seg Mai 26, 2014 22:42
por e8group » Seg Mai 26, 2014 22:42
Ok.
Nós temos que
![3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \cdot 3^{1-x} \left( 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right) \iff 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \left( 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] \right) 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \cdot 3^{1-x} \left( 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right) \iff 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \left( 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] \right)](/latexrender/pictures/ddcc25b90ebb2f9b787b7e1c5e39b708.png)
Agora , aplicando a distributividade em relação a soma ,
![3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] = 3^{1-x} \cdot 3^{x-1} - 3^{1-x} \cdot 3^{x} + 3^{1-x} \cdot 3^{x+1} + 3^{1-x} \cdot 3^{x+2} 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] = 3^{1-x} \cdot 3^{x-1} - 3^{1-x} \cdot 3^{x} + 3^{1-x} \cdot 3^{x+1} + 3^{1-x} \cdot 3^{x+2}](/latexrender/pictures/e930ff311fae1925107afc287881b84e.png)
. Utilizando a propriedade
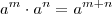
,segue
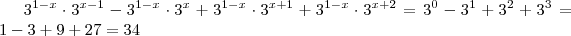
.
Entendeu ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1622 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2830 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2822 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2238 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2187 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
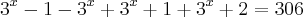
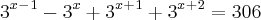
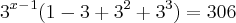 (Porque tem aquele 1 dentro dos parênteses? como ficou assim?)
(Porque tem aquele 1 dentro dos parênteses? como ficou assim?)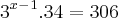 (Porque 34? )
(Porque 34? )

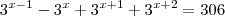 ? Se sim , note que podemos multiplicar a eq. por 1, vejamos que
? Se sim , note que podemos multiplicar a eq. por 1, vejamos que 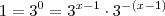 e
e 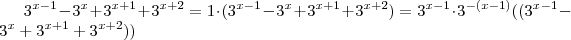
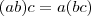 + a distributiva
+ a distributiva 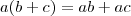 , resulta
, resulta 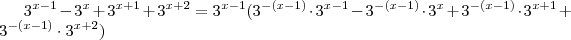 .
. 
![3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \cdot 3^{1-x} \left( 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right) \iff 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \left( 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] \right) 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \cdot 3^{1-x} \left( 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right) \iff 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} = 3^{x-1} \left( 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] \right)](/latexrender/pictures/ddcc25b90ebb2f9b787b7e1c5e39b708.png)
![3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] = 3^{1-x} \cdot 3^{x-1} - 3^{1-x} \cdot 3^{x} + 3^{1-x} \cdot 3^{x+1} + 3^{1-x} \cdot 3^{x+2} 3^{1-x}\left[ 3^{x-1} - 3^x + 3^{x+1} + 3^{x+2} \right] = 3^{1-x} \cdot 3^{x-1} - 3^{1-x} \cdot 3^{x} + 3^{1-x} \cdot 3^{x+1} + 3^{1-x} \cdot 3^{x+2}](/latexrender/pictures/e930ff311fae1925107afc287881b84e.png) . Utilizando a propriedade
. Utilizando a propriedade 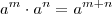 ,segue
,segue 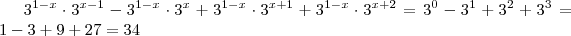 .
. 