 por eu_dick1 » Sex Mai 23, 2014 14:16
por eu_dick1 » Sex Mai 23, 2014 14:16
Galera, estou com uma seguinte dúvida:
![A= ]-\infty;8] A= ]-\infty;8]](/latexrender/pictures/c6361ee25c15154ca65b2dc703e7c2cd.png)
e

.
Como os intervalos vão até o menos infinito, não incluindo o menos infinito e até mais infinito, não incluindo o infinito, eu posso dizer que
![A \cup B= ]-\infty;\infty[ A \cup B= ]-\infty;\infty[](/latexrender/pictures/3c0a8a05ac4bee06f4d891d5404eeb3a.png)
?
-
eu_dick1
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mai 17, 2014 01:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: formado
 por alienante » Sex Mai 23, 2014 16:18
por alienante » Sex Mai 23, 2014 16:18
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por eu_dick1 » Sex Mai 23, 2014 20:30
por eu_dick1 » Sex Mai 23, 2014 20:30
Alienante, eu não entendi esse
![-]8;10[ -]8;10[](/latexrender/pictures/53cbb8e4a6dd03b99d2f7e3ed91ee695.png)
, você poderia me explicar?
-
eu_dick1
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mai 17, 2014 01:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: formado
 por eu_dick1 » Sex Mai 23, 2014 21:21
por eu_dick1 » Sex Mai 23, 2014 21:21
Ah, eu tenho uma correção, eu errei no exercício, na verdade é:
![A= ]-\infty;8[ e B= [10;\infty[. A= ]-\infty;8[ e B= [10;\infty[.](/latexrender/pictures/01c2940850028aa6d3594f07c1bdc8ec.png)
Deixa eu ver se entendi a lógica... ficaria
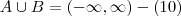
?
-
eu_dick1
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mai 17, 2014 01:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: formado
 por alienante » Sáb Mai 24, 2014 21:09
por alienante » Sáb Mai 24, 2014 21:09
percaba que se voce colocar os conjuntos

e

voce verá que há um "rombo" que é justamente o intervalo
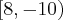
(perceba que o oito não faz parte do conjunto

), então se esse intervalo não está contido em nenhum dos dois conjuntos, portanto quando se fizer a união dos dois ele tambem não irá estar incluído logo a resposta será toda a reta exceto esse intervalo:

.
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [União de 4 Conjuntos]
por ofhell » Qui Mai 03, 2012 13:54
- 1 Respostas
- 4056 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 00:02
Conjuntos
-
- Probabilidade da união
por Malorientado » Qua Set 19, 2012 22:58
- 5 Respostas
- 13676 Exibições
- Última mensagem por fraol

Sáb Set 22, 2012 12:34
Probabilidade
-
- União/Interseção de Conjuntos
por joaofonseca » Qui Jan 10, 2013 00:28
- 1 Respostas
- 2605 Exibições
- Última mensagem por fraol

Seg Fev 11, 2013 17:41
Conjuntos
-
- duvida em união interseção de um conjunto
por kzacristo19 » Seg Ago 26, 2013 01:08
- 0 Respostas
- 1502 Exibições
- Última mensagem por kzacristo19

Seg Ago 26, 2013 01:08
Conjuntos
-
- [Problemas] Relação entre união e interseção
por amandasousa_m » Qui Ago 15, 2013 08:59
- 1 Respostas
- 3903 Exibições
- Última mensagem por MateusL

Sex Ago 16, 2013 12:46
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![A= ]-\infty;8] A= ]-\infty;8]](/latexrender/pictures/c6361ee25c15154ca65b2dc703e7c2cd.png) e
e  .
.![A \cup B= ]-\infty;\infty[ A \cup B= ]-\infty;\infty[](/latexrender/pictures/3c0a8a05ac4bee06f4d891d5404eeb3a.png) ?
?
![A= ]-\infty;8] A= ]-\infty;8]](/latexrender/pictures/c6361ee25c15154ca65b2dc703e7c2cd.png) e
e  .
.![A \cup B= ]-\infty;\infty[ A \cup B= ]-\infty;\infty[](/latexrender/pictures/3c0a8a05ac4bee06f4d891d5404eeb3a.png) ?
?

![-]8;10[ -]8;10[](/latexrender/pictures/53cbb8e4a6dd03b99d2f7e3ed91ee695.png) , você poderia me explicar?
, você poderia me explicar?
![A= ]-\infty;8[ e B= [10;\infty[. A= ]-\infty;8[ e B= [10;\infty[.](/latexrender/pictures/01c2940850028aa6d3594f07c1bdc8ec.png)
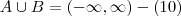 ?
?
 e
e  voce verá que há um "rombo" que é justamente o intervalo
voce verá que há um "rombo" que é justamente o intervalo 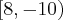 (perceba que o oito não faz parte do conjunto
(perceba que o oito não faz parte do conjunto  ), então se esse intervalo não está contido em nenhum dos dois conjuntos, portanto quando se fizer a união dos dois ele tambem não irá estar incluído logo a resposta será toda a reta exceto esse intervalo:
), então se esse intervalo não está contido em nenhum dos dois conjuntos, portanto quando se fizer a união dos dois ele tambem não irá estar incluído logo a resposta será toda a reta exceto esse intervalo: .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

