O MMC entre
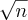
e
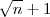
é
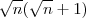
.
Os estudantes de matemática, em geral, apresentam uma certa dificuldade quanto a efetuar somas de frações em virtude de, além de (na maioria dos casos) não compreenderem muito bem o conceito envolvido no MMC, ter preguiça de calculá-lo. De fato, é um cálculo extenso. Eu mesmo nunca o faço para efetuar frações. Ao invés de tomar o denominador da soma das frações como o MMC dos denominadores das parcelas o tomo, simplesmente, pelo
produto dos denominadores. Não há absolutamente perda nenhuma de generalidade nesse método.
De fato, para quaisquer Reais

,

,

e
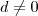
é verdade que
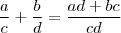
.
Tente resolver assim, se preferir. Neste caso específico não tem graça pois o MMC
coincide com o produto dos denominadores. Isto acontecerá sempre que os denominadores forem
primos entre si.
![\frac{1}{\sqrt[]{n}} - \frac{1}{\sqrt[]{n}+1} \frac{1}{\sqrt[]{n}} - \frac{1}{\sqrt[]{n}+1}](/latexrender/pictures/0a9448f219505e3a84e5ebf71177968f.png) é equivalente a:
é equivalente a:![\frac{n-\sqrt[]{n}}{n(n-1)} \frac{n-\sqrt[]{n}}{n(n-1)}](/latexrender/pictures/4141a2f7e3a6c1a0bad29a47ab2acf32.png)
![\frac{\sqrt[]{n}-1}{n(n-1)} \frac{\sqrt[]{n}-1}{n(n-1)}](/latexrender/pictures/6a06ccf75e5d9ac90ed62e4d9ab8b18e.png)
![\frac{\sqrt[]{n}}{n+\sqrt[]{n}} \frac{\sqrt[]{n}}{n+\sqrt[]{n}}](/latexrender/pictures/4a04d9ed0622436732ac49fa6e9e6d6d.png)
![\frac{\sqrt[]{n}}{n} \frac{\sqrt[]{n}}{n}](/latexrender/pictures/7db67835cadbece31e264c73d9f5e618.png)
![\frac{\sqrt[]{n}-n}{n+1} \frac{\sqrt[]{n}-n}{n+1}](/latexrender/pictures/096e6a9dd5782a9eef8c95a945ab6612.png)

![\frac{1}{\sqrt[]{n}} - \frac{1}{\sqrt[]{n}+1} \frac{1}{\sqrt[]{n}} - \frac{1}{\sqrt[]{n}+1}](/latexrender/pictures/0a9448f219505e3a84e5ebf71177968f.png) é equivalente a:
é equivalente a:![\frac{n-\sqrt[]{n}}{n(n-1)} \frac{n-\sqrt[]{n}}{n(n-1)}](/latexrender/pictures/4141a2f7e3a6c1a0bad29a47ab2acf32.png)
![\frac{\sqrt[]{n}-1}{n(n-1)} \frac{\sqrt[]{n}-1}{n(n-1)}](/latexrender/pictures/6a06ccf75e5d9ac90ed62e4d9ab8b18e.png)
![\frac{\sqrt[]{n}}{n+\sqrt[]{n}} \frac{\sqrt[]{n}}{n+\sqrt[]{n}}](/latexrender/pictures/4a04d9ed0622436732ac49fa6e9e6d6d.png)
![\frac{\sqrt[]{n}}{n} \frac{\sqrt[]{n}}{n}](/latexrender/pictures/7db67835cadbece31e264c73d9f5e618.png)
![\frac{\sqrt[]{n}-n}{n+1} \frac{\sqrt[]{n}-n}{n+1}](/latexrender/pictures/096e6a9dd5782a9eef8c95a945ab6612.png)

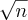 e
e 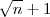 é
é 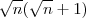 .
.  ,
, ,
, e
e 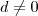 é verdade que
é verdade que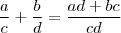 .
.
![\frac{\sqrt[]{n}+1-\sqrt[]{n}}{\sqrt[]{n}(\sqrt[]{n}+1)} \frac{\sqrt[]{n}+1-\sqrt[]{n}}{\sqrt[]{n}(\sqrt[]{n}+1)}](/latexrender/pictures/04c2dc06b1193fb567a6476aced4f054.png)
![= \frac{1}{\sqrt[]{n}(\sqrt[]{n}+1)} = \frac{1}{\sqrt[]{n}(\sqrt[]{n}+1)}](/latexrender/pictures/27b5105c594861fecb3dc3037a1b194d.png)
![= \frac{1}{n+\sqrt[]{n}} = \frac{1}{n+\sqrt[]{n}}](/latexrender/pictures/2a493149a69fe78c27f8993946c5fd5a.png)
![= \frac{1}{n+\sqrt[]{n}} . \frac{n-\sqrt[]{n}}{n-\sqrt[]{n}} = \frac{1}{n+\sqrt[]{n}} . \frac{n-\sqrt[]{n}}{n-\sqrt[]{n}}](/latexrender/pictures/f9b322e64531f9b61c3f2c5cfcf7cb31.png)
![= \frac{n-\sqrt[]{n}}{{n}^{2}-n} = \frac{n-\sqrt[]{n}}{{n}^{2}-n}](/latexrender/pictures/741906c07553ffdb5e8dc3856ebd4ee7.png)
![= \frac{n-\sqrt[]{n}}{n(n-1)} = \frac{n-\sqrt[]{n}}{n(n-1)}](/latexrender/pictures/0cd00ccd3ed0d32bf46bccbbf7a1ca05.png)


 .
.



