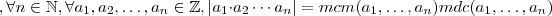Tudo acima está certo , só acrescentando ...
Há um grande resultado que estabelece a igualdade
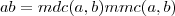
.(Embora não pede-se a dedução desta fórmula ,já que sugerir a aplicação da mesma vou postar a minha interpretação de como a mesma foi obtida , que não necessariamente é a mais adequada aos padrões de Teoria do Números uma vez que ainda não estudei isto )
Se quiser ir direto ao ponto ignore a dedução da mesma .
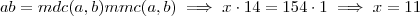
(que condiz com a resposta por Russman )
Obtendo a fórmula .
Seja

inteiros. Seja
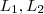
o conjuntos de todos os múltiplos (positivos ) de

e

respectivamente .
O menor elemento ,digamos

, que está na interseção de
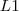
por

é minimo múltiplo comum de

e

, isto é ,
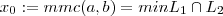
.
Pelo Teorema fundamental da aritmética (
http://pt.wikipedia.org/wiki/Teorema_fu ... %C3%A9tica) , existe
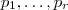
primos distintos e inteiros
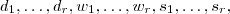
não negativos tais que
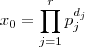
.
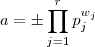
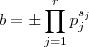
.
Segue como definimos

que
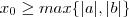
, logo para cada
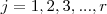
temos
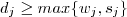
. Mas pela minimalidade de

,obtemos
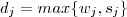
e assim ,
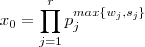
.
Observe que é isto que fazemos para descobrir o mmc entre números
50 =
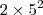
40 =
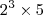
L_1 : 50,100,150, 200,...
L_2: 40,80,120 ,160,200 ,...
e 200 =
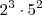
Agora sendo mais breve possível ...
E se

fosse o maior divisor de

(isto é
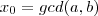
) ?
R.Teríamos
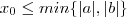
e isto implicaria que
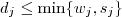
, mas pela maximalidade de

(pois ele é o maior divisor de a e b ) obteríamos
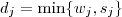
. Assim ,
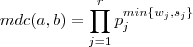
.
Consequência :
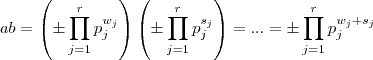
. Mas é claro que
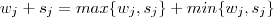
e com isso
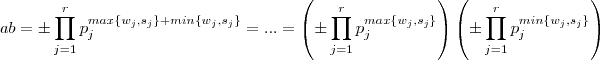
e obtemos a fórmula .


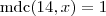 então
então  não é múltiplo de
não é múltiplo de  e nem de
e nem de  . É o mesmo que dizer que
. É o mesmo que dizer que  e
e 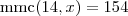 então deve existir
então deve existir  tal que
tal que 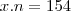 . Mas, como
. Mas, como 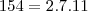 e
e  .
.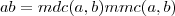 .(Embora não pede-se a dedução desta fórmula ,já que sugerir a aplicação da mesma vou postar a minha interpretação de como a mesma foi obtida , que não necessariamente é a mais adequada aos padrões de Teoria do Números uma vez que ainda não estudei isto )
.(Embora não pede-se a dedução desta fórmula ,já que sugerir a aplicação da mesma vou postar a minha interpretação de como a mesma foi obtida , que não necessariamente é a mais adequada aos padrões de Teoria do Números uma vez que ainda não estudei isto ) 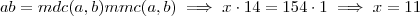 (que condiz com a resposta por Russman )
(que condiz com a resposta por Russman )  inteiros. Seja
inteiros. Seja 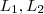 o conjuntos de todos os múltiplos (positivos ) de
o conjuntos de todos os múltiplos (positivos ) de  e
e  respectivamente .
respectivamente .  , que está na interseção de
, que está na interseção de 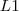 por
por  é minimo múltiplo comum de
é minimo múltiplo comum de 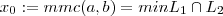 .
.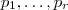 primos distintos e inteiros
primos distintos e inteiros 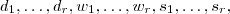 não negativos tais que
não negativos tais que 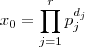 .
.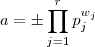
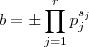 .
. 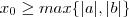 , logo para cada
, logo para cada 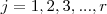 temos
temos 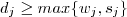 . Mas pela minimalidade de
. Mas pela minimalidade de 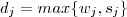 e assim ,
e assim , 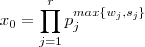 .
. 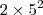
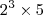
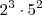
 (isto é
(isto é 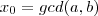 ) ?
) ?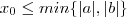 e isto implicaria que
e isto implicaria que 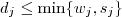 , mas pela maximalidade de
, mas pela maximalidade de 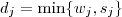 . Assim ,
. Assim , 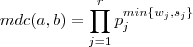 .
. 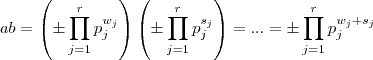 . Mas é claro que
. Mas é claro que 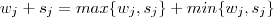 e com isso
e com isso 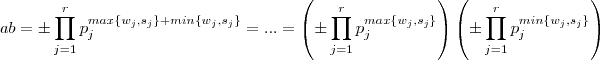 e obtemos a fórmula .
e obtemos a fórmula .