 por ilane » Seg Mai 05, 2014 14:40
por ilane » Seg Mai 05, 2014 14:40
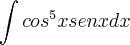
Calculei usando a substituição e seguei a um resultado mais um colega me disse que estava errado podem me ajudar a sanar essa dúvida em relação a substituição cheguei no seguinte resultado;
\frac{-1}{6} cos^6 (x) + c
-
ilane
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Abr 08, 2014 10:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por KleinIll » Seg Mai 05, 2014 15:57
por KleinIll » Seg Mai 05, 2014 15:57
Sua resposta está correta.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por ilane » Seg Mai 05, 2014 16:38
por ilane » Seg Mai 05, 2014 16:38
KleinIll escreveu:Sua resposta está correta.
Qual a certeza que você me dá para que a resposta esteja correta?
-
ilane
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Abr 08, 2014 10:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por KleinIll » Seg Mai 05, 2014 16:55
por KleinIll » Seg Mai 05, 2014 16:55
Você pensou corretamente. Veja como eu fiz:
Se você assumir que a = cos(x). A derivada de a é: da = -sen(x)dx
Substituindo na integral você chegará em: Int( a^5 * (-1) * da )
Integrando -a^5 em função de a = -1/6 * a^6 + c, porém a = cos(x), então o resultado é (-1/6) * (cos(x))^6 + c.
Entendeu?
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2866 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
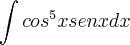 Calculei usando a substituição e seguei a um resultado mais um colega me disse que estava errado podem me ajudar a sanar essa dúvida em relação a substituição cheguei no seguinte resultado;
Calculei usando a substituição e seguei a um resultado mais um colega me disse que estava errado podem me ajudar a sanar essa dúvida em relação a substituição cheguei no seguinte resultado;
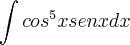 Calculei usando a substituição e seguei a um resultado mais um colega me disse que estava errado podem me ajudar a sanar essa dúvida em relação a substituição cheguei no seguinte resultado;
Calculei usando a substituição e seguei a um resultado mais um colega me disse que estava errado podem me ajudar a sanar essa dúvida em relação a substituição cheguei no seguinte resultado;


