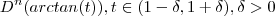 para determinar
para determinar  de modo que o erro da aproximação de
de modo que o erro da aproximação de  por
por 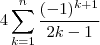 seja menor que
seja menor que  .
.Alguém tem alguma ideia ? Como obter uma expressão para
 ?
? Até agora só consegui isto abaixo ...
i) Primeiro vamos garantir que
 é limitada em
é limitada em  .
.Derivando
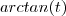 n-vezes , vamos obter uma expressão da forma
n-vezes , vamos obter uma expressão da forma  ,onde
,onde  é um polinômio
é um polinômio 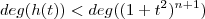 e portanto
e portanto 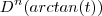 é uma função racional e
é uma função racional e  .Sendo assim garantimos que
.Sendo assim garantimos que 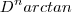 é contínua .Em particular , ela é contínua em qualquer intervalo fechado não degenerado contendo a vizinhança de
é contínua .Em particular , ela é contínua em qualquer intervalo fechado não degenerado contendo a vizinhança de  .Logo pelo Teorema de Weierstrass ,
.Logo pelo Teorema de Weierstrass , 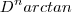 é limitada neste intervalo .
é limitada neste intervalo . Assim ,

ii) Segunda parte trabalhosa, determinar
 e encontrar uma cota .
e encontrar uma cota . Pensei assim :
Seja
![I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right) I_n (t) = D^n(arctan(t)) = D^n \left(\int_0^t \frac{d\zeta }{1+ \zeta^2}\right) = \frac{1}{2i}D^n \left(\int_0^t \left[ \frac{1 }{t -i} - \frac{1 }{t +i} \right ]d \zeta \right)](/latexrender/pictures/d7c19ec5b41f47b62c610c156d7f5e04.png)
Daí , temos
![I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right] I_n(t) = \frac{1}{2i}(-1)^n n! \left[ \frac{1}{(t-i)^{n+1}} - \frac{1}{(t+i)^{n+1}}\right ] = \frac{i}{2}(-1)^{n+1} \frac{n!}{(t+1)^{n+1}}\left[ (t+i)^{n+1}- (t-i)^{n+1}\right]](/latexrender/pictures/6b7f2ca704f1991f83afbb2817ea8384.png) e finalmente obtemos
e finalmente obtemos ![I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k} I_n(t) = \frac{(-1)^{n+1}n!}{2(1+t)^{n+1}} \sum_{m=0}^{n+1} \binom{n+1}{m}[1-(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}](/latexrender/pictures/45dcf87ee4c76edf4cbac4078fde283f.png) .
. Logo ,
![|I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2} |I_n(t)| = \frac{n!}{2(1+t)^{n+1}} | \sum_{m=0}^{n+1} \binom{n+1}{m}[1+(-1)^{m+1}]i^{k+1} \cdot t^{n+1 -k}| \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m}|(1-(-1)^{m+1})i^{k+1}|t^{n+1-k} \leq \frac{n!}{2(1+t)^{n+1}} \cdot \sum_{m=0}^{n+1} \binom{n+1}{m} t^{n+1-k} = \frac{n!}{2(1+t)^{n+1}} \cdot (1+t)^{n+1} = \frac{n!}{2}](/latexrender/pictures/0726c60a3f905901b0974c49e518fa79.png) .
. Portanto
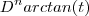 é limitada por
é limitada por 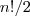 .
. Mas esta cota não ajuda , meu objetivo era obter
 .
. iii) Encontrar
 .
. Sabemos que
 (Forma Lagrange). , então
(Forma Lagrange). , então  , .
, .Se tivéssemos demostrado que
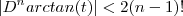 .
.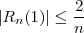 e com isso
e com isso 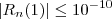 sempre que
sempre que  que é a resposta do gabarito .
que é a resposta do gabarito .Qualquer ajuda é bem vinda .

