 por kaic » Seg Abr 07, 2008 23:48
por kaic » Seg Abr 07, 2008 23:48
Preciso de ajuda!
Não consigo resolver essa expressão.
% MathType!MTEF!2!1!+-
% feqaeaartrvr0aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l
% bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R
% Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa
% caGaaeqabaaaamaaaOqaaiaaisdacaGGUaWaaeWaaeaadaWcaaqaai
% aaigdaaeaacaaIYaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaaGin
% aaaakiabgUcaRmaabmaabaWaaSaaaeaacaaIXaaabaGaaGinaaaaai
% aawIcacaGLPaaadaahaaWcbeqaamaalaaabaGaaGymaaqaaiaaikda
% aaaaaOGaeyypa0daaa!3DD2!
$4.\left( {\frac{1}{2}} \right)^4 + \left( {\frac{1}{4}} \right)^{\frac{1}{2}} = $
-
kaic
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 07, 2008 22:19
- Área/Curso: Estudante
- Andamento: cursando
 por kaic » Seg Abr 07, 2008 23:52
por kaic » Seg Abr 07, 2008 23:52
% MathType!MTEF!2!1!+-
% feqaeaartrvr0aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l
% bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R
% Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa
% caGaaeqabaaaamaaaOqaaiaadIhacqGH9aqpcaaIYaWaaOaaaeaaca
% aIYaGaaGinaiabgkHiTmaakaaabaGaaGynaiaaisdacqGH9aqpaSqa
% baaabeaaaaa!3979!
$x = 2\sqrt {24 - \sqrt {54 = } } $
-
kaic
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 07, 2008 22:19
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Abr 08, 2008 00:08
por admin » Ter Abr 08, 2008 00:08
Olá
kaic, seja bem-vindo!
Os códigos adicionais do MathType não são reconhecidos dentro do BBCode tex do LaTeX.
Ao enviar fórmulas, confira se estão como você deseja através do botão "Prever" antes da postagem, ou através do "Editor de Fórmulas".
Favor verificar se era assim que desejava escrever (repare o código dentro da tag tex):
- Código: Selecionar todos
[tex]4.\left( {\frac{1}{2}} \right)^4 + \left( {\frac{1}{4}} \right)^{\frac{1}{2}} = [/tex]
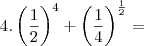
- Código: Selecionar todos
[tex]x = 2\sqrt {24 - \sqrt {54 } }=[/tex]

-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por kaic » Ter Abr 08, 2008 02:33
por kaic » Ter Abr 08, 2008 02:33
Fábio
Obrigado
São essas duas espressões mesmo, desculpe baixei o programa mais não sei mexer, ainda não tive tempo estou atolado de expressões para fazer.
Valeu!
-
kaic
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 07, 2008 22:19
- Área/Curso: Estudante
- Andamento: cursando
 por kaic » Ter Abr 08, 2008 03:04
por kaic » Ter Abr 08, 2008 03:04
Fábio
Tentei fazer de todas as maneiras as duas questões, o problema e que a professora passou a resposta dos dois, e por mais que eu faça não obtenho o resultado correto.
Gostaria que você me ensina se como fazer, já fatorei, fiz mmc, extrai raiz e não consigo.
Valeu
-
kaic
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 07, 2008 22:19
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Abr 08, 2008 05:04
por admin » Ter Abr 08, 2008 05:04
O expoente meio equivale à raiz quadrada. Tente reescrever a primeira expressão assim.
Seus tópicos foram mesclados, confira novamente a segunda expressão.
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressoes
por Biinha » Ter Fev 19, 2013 16:55
- 4 Respostas
- 2434 Exibições
- Última mensagem por Biinha

Sex Fev 22, 2013 11:41
Conjuntos
-
- expressoes
 por Bernardo Silva » Sáb Nov 19, 2016 16:40
por Bernardo Silva » Sáb Nov 19, 2016 16:40
- 1 Respostas
- 1622 Exibições
- Última mensagem por Jadiel Carlos

Seg Nov 21, 2016 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [expressões] problema
por Cleyson007 » Ter Jul 01, 2008 01:43
- 9 Respostas
- 16491 Exibições
- Última mensagem por paulo testoni

Qua Out 01, 2008 16:23
Álgebra Elementar
-
- Cálculo de Expressões
por Jansen » Dom Ago 30, 2009 01:28
- 2 Respostas
- 2815 Exibições
- Última mensagem por Jansen

Dom Ago 30, 2009 17:17
Sistemas de Equações
-
- Simplicando expressões
por Florisbela » Dom Mai 23, 2010 19:48
- 1 Respostas
- 1443 Exibições
- Última mensagem por DanielFerreira

Ter Jun 08, 2010 18:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


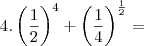


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.