amigao , cometi um erro , não sei por que fiz aquilo , a definição é clara. O fato de
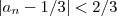
não implica que
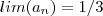
. É claro que

sempre que

(Vimos isto ) . Mas , se
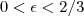
? Será que existe
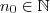
t.q

?
Por definição

. Isto deve funcionar para todo

e não apenas para um em particular conforme eu fiz .
Quando
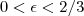
, parece complicado determinar um

correspondente t.q .

. Entretanto , podemos limitar

(inferiormente e superiormente) por duas sequências convergente para
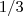
(em que a demostração seja mais simples ) e com isso pelo teorema do confronto

.
Já vimos que

e hoje afirmo que
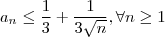
. (A verificação é simples , o denominador de

é sempre maior que

, logo a relação de ordem inverte em relação ao recíproco )
Seja :
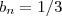
e
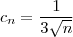
e
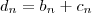
. Portanto , temos
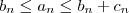
.
Provar a convergência de

é simples (comparado com
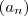
) e provar a convergência de
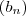
trivial .
Provando isto acima

converge para a soma dos limites de
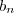
e
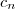
.
Para a resposta não ficar vaga , vou propor uma demostração para dois teoremas (acho mais fácil que provar que (a_n) converge [/tex] .
Teorema 1 :
Sejam

e a sequência

d_n := b_n + c_n [/tex] .
Se

e
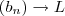
então

.
Prova :
Da hipótese

e
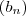
convergirem , dado qualquer

existe
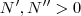
tais que
(1)

sempre que
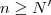
(2)

sempre que

Agora
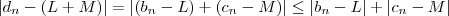
. Podemos definir
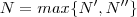
com isso (1) e (2) são simultaneamente verdadeiros sempre que
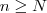
, donde resulta por transitividade que
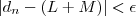
.
Teorema 2 :
Se existe

tal que

para todo
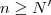
e
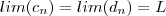
, logo

.Prova :
Dá hipótese
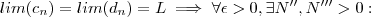
(1)

(2)
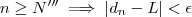
.
Seja

, então (1), (2) e

são sempre verdadeiros quando
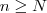
.
Como
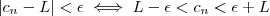
e
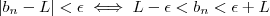
, então por transitividade

sempre que
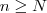
.


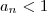 , basta notar que o número do numerador é sempre menor que do denominador e portanto o quociente é menor que 1 .
, basta notar que o número do numerador é sempre menor que do denominador e portanto o quociente é menor que 1 .  , note que
, note que 
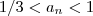 para qualquer
para qualquer  natural . Então ,
natural . Então , 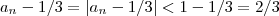 . Pondo ,
. Pondo ,  e
e  , obtemos
, obtemos  tal que
tal que  implica
implica  .
.

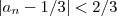 não implica que
não implica que 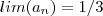 . É claro que
. É claro que  sempre que
sempre que  (Vimos isto ) . Mas , se
(Vimos isto ) . Mas , se 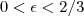 ? Será que existe
? Será que existe 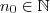 t.q
t.q  ?
?  . Isto deve funcionar para todo
. Isto deve funcionar para todo 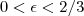 , parece complicado determinar um
, parece complicado determinar um  correspondente t.q .
correspondente t.q .  . Entretanto , podemos limitar
. Entretanto , podemos limitar  (inferiormente e superiormente) por duas sequências convergente para
(inferiormente e superiormente) por duas sequências convergente para 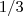 (em que a demostração seja mais simples ) e com isso pelo teorema do confronto
(em que a demostração seja mais simples ) e com isso pelo teorema do confronto  .
.  e hoje afirmo que
e hoje afirmo que 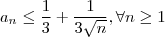 . (A verificação é simples , o denominador de
. (A verificação é simples , o denominador de  , logo a relação de ordem inverte em relação ao recíproco )
, logo a relação de ordem inverte em relação ao recíproco )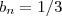 e
e 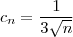 e
e 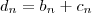 . Portanto , temos
. Portanto , temos 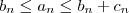 .
.  é simples (comparado com
é simples (comparado com 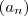 ) e provar a convergência de
) e provar a convergência de 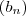 trivial .
trivial .  converge para a soma dos limites de
converge para a soma dos limites de 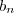 e
e 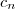 .
.  e a sequência
e a sequência  d_n := b_n + c_n [/tex] .
d_n := b_n + c_n [/tex] . e
e 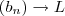 então
então  .
. 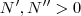 tais que
tais que  sempre que
sempre que 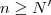
 sempre que
sempre que 
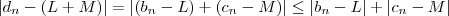 . Podemos definir
. Podemos definir 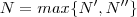 com isso (1) e (2) são simultaneamente verdadeiros sempre que
com isso (1) e (2) são simultaneamente verdadeiros sempre que 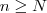 , donde resulta por transitividade que
, donde resulta por transitividade que 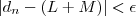 .
.  tal que
tal que  para todo
para todo 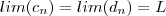 , logo
, logo  .Prova :
.Prova : 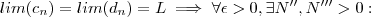

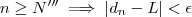 .
.  , então (1), (2) e
, então (1), (2) e 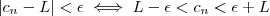 e
e 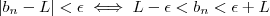 , então por transitividade
, então por transitividade  sempre que
sempre que  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
