problema

[rcpn]

O gerente de um supermercado pediu para organizar as latas de chocolate em pó em uma pilha triangular de modo que no último andar tenha uma lata e no penúltimo três latas, e que o número de lata em cada andar represente os números triangulares. Sabendo que há no estoque 220 latas de chocolate em pó. Quantos andares terão uma pilha.

Caros amigos! Achei essa questão muito estranha porque ele diz para analisarmos a pirâmide de números que tem 1 lata na última pilha e 3 latas na penúltima pilha. De 1 ele passou para 3, mas acontece a relação de números triangulares obedece a regra a partir de 3 números em diante podendo misturar números pares e ímpares. Em nenhum desses casos eu consegui encontrar uma forma de saber que 220 latas são capazes de formar 10 pilhas que é a resposta. Gostaria de ajuda. Acho que não formam 10 pilhas, e sim 20 pilhas. De qualquer forma, agradeço a atenção dos amigos.

[Russman]

Se o número de andares coincidir com o n-ésimo número triangular então 210 latas formarão 20 andares.

Porém, parece q o exercício tem uma sutileza. No primeiro andar temos uma lata. No segundo, 3 lastas. Assim, a soma do primeiro andar com o segundo andar é 4. Portanto, ao fim de P pilhas precisamos somar os P primeiros números triangulares. Essa soma é



de onde

.

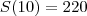
Dez pilhas contém, exatamente, 220 latas.