1.a)
![\[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\]](/latexrender/pictures/eea988cefbcd315c934c93484090657e.png)
1.c)
![\[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\]](/latexrender/pictures/2f7b5ccc871e8ef61d782b9d368b8d0a.png)
1.e)
![\[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\] \[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\]](/latexrender/pictures/122c9e49ad78499eddadbd65d027ec00.png)
3.b)
![\[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\]](/latexrender/pictures/477bda5e72f2256038bde29b1f8ce445.png) cuidado para NÃO CONFUNDIR com
cuidado para NÃO CONFUNDIR com ![\[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\]](/latexrender/pictures/69bffcf179848289e32d255c49b2f2dc.png) (esse eu já sei resolver)
(esse eu já sei resolver)Se alguém puder me ajudar...

![\[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\]](/latexrender/pictures/eea988cefbcd315c934c93484090657e.png)
![\[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\]](/latexrender/pictures/2f7b5ccc871e8ef61d782b9d368b8d0a.png)
![\[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\] \[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\]](/latexrender/pictures/122c9e49ad78499eddadbd65d027ec00.png)
![\[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\]](/latexrender/pictures/477bda5e72f2256038bde29b1f8ce445.png) cuidado para NÃO CONFUNDIR com
cuidado para NÃO CONFUNDIR com ![\[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\]](/latexrender/pictures/69bffcf179848289e32d255c49b2f2dc.png) (esse eu já sei resolver)
(esse eu já sei resolver)
 qualquer número real não nulo , o limite
qualquer número real não nulo , o limite 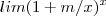 vale
vale  (podendo
(podendo 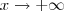 quanto a
quanto a  )
)  e com isso
e com isso 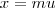 . Quando
. Quando 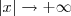 temos que
temos que  também tende a
também tende a  .Das duas uma ,
.Das duas uma , 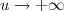 ou
ou 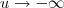 ( o sinal de
( o sinal de  que diz isso ) e assim
que diz isso ) e assim ![lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m](/latexrender/pictures/0b58087e368df4ea87d182f2ebe2aa80.png) . Por definição
. Por definição 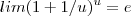 (podendo
(podendo 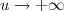 quanto a
quanto a  ) . Daí , o limite de expressões da forma
) . Daí , o limite de expressões da forma  (
(  ) terá sempre como resultado
) terá sempre como resultado 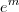 .
. 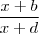 elevado a x ,
elevado a x ,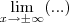 .
.  .
.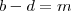 e
e 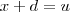 . Quando
. Quando  temos que
temos que 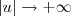 e
e 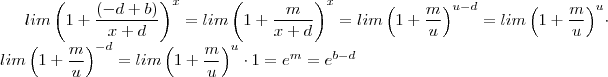 (utilizando o resultado anterior)
(utilizando o resultado anterior)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes

 .
.



