 por mateushamm » Dom Abr 13, 2014 14:35
por mateushamm » Dom Abr 13, 2014 14:35
Olá, pessoal
Por que a raíz de um número não pode ser negativa?
Por exemplo, por que a raíz quadrada de 9 não pode ser -3? Afinal (-3) * (-3) = 9. E uma raiz quadrada de um número x é um número que, quando multiplicado por si próprio, iguala x.
Grato
-
mateushamm
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Abr 13, 2014 14:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por BrenoNaval » Dom Abr 13, 2014 21:59
por BrenoNaval » Dom Abr 13, 2014 21:59
A raiz quadrada de um número positivo é +ou - seu valor,com no exemplo
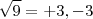
, porém o que pode vir a confundir é a raiz quadrada de um número negativo,pois não está contido no conjunto dos números reais.
Oberve.:
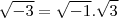
(chamando
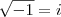
) teremos que
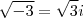
Para lidarmos com isso,foi criado uma sequência.:

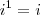
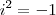
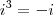
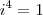
.
.
.
No entanto por ''i'' pertencer ao conjunto dos números complexos não é muito usual utilizar raízes negativas em exercícios,pois o conjunto dos números complexos está separado do conjunto dos números reais que vem a ser o mais utilizado.
Editado pela última vez por
BrenoNaval em Dom Abr 13, 2014 22:34, em um total de 8 vezes.
-
BrenoNaval
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 30, 2014 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Abr 13, 2014 22:11
por Russman » Dom Abr 13, 2014 22:11
A raiz quadrada de
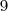
é

OU
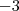
. Onde você leu que a raiz de um número não pode ser negativa?
O que não existe é um resultado real para a
extração da raiz quadrada de um numero negativo.
Por exemplo, a operação
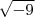
não tem resultado real. Isto é, não existe nenhum número pertencente ao conjunto dos números reais tal que o seu produto por si mesmo calcule
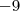
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3436 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
-
- [Porcentagem negativa.]
por felipel » Sex Jul 25, 2014 11:15
- 0 Respostas
- 3445 Exibições
- Última mensagem por felipel

Sex Jul 25, 2014 11:15
Matemática Financeira
-
- seno e secante negativa
por Apotema » Seg Nov 23, 2009 14:36
- 2 Respostas
- 1986 Exibições
- Última mensagem por Apotema

Qua Nov 25, 2009 16:54
Trigonometria
-
- [POTENCIAÇÃO] BASE NEGATIVA
por anneliesero » Seg Jan 28, 2013 15:34
- 1 Respostas
- 1469 Exibições
- Última mensagem por Russman

Seg Jan 28, 2013 18:15
Álgebra Elementar
-
- Fação impropria negativa, na forma mista
por LuizCarlos » Sáb Mar 17, 2012 02:15
- 5 Respostas
- 3280 Exibições
- Última mensagem por LuizCarlos

Dom Mar 18, 2012 20:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


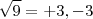 , porém o que pode vir a confundir é a raiz quadrada de um número negativo,pois não está contido no conjunto dos números reais.
, porém o que pode vir a confundir é a raiz quadrada de um número negativo,pois não está contido no conjunto dos números reais.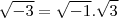 (chamando
(chamando 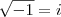 ) teremos que
) teremos que 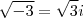

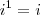
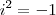
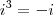
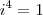
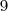 é
é  OU
OU 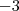 . Onde você leu que a raiz de um número não pode ser negativa?
. Onde você leu que a raiz de um número não pode ser negativa?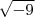 não tem resultado real. Isto é, não existe nenhum número pertencente ao conjunto dos números reais tal que o seu produto por si mesmo calcule
não tem resultado real. Isto é, não existe nenhum número pertencente ao conjunto dos números reais tal que o seu produto por si mesmo calcule 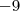 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
