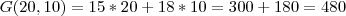por rcpn » Ter Abr 08, 2014 11:03
por rcpn » Ter Abr 08, 2014 11:03
UMA DONA DE CASA COMPRA CARNE E PEIXE, NUM TOTAL DE MENSAL DE 30KG. O PREÇO DE CADA KG DE CARNE É 15 REAIS E CADA KG DE PEIXE É 18 REAIS. PEDE-SE:
a) O GASTO DE 1 MÊS EM QUE A DONA DE CASA COMPROU 10 KG DE PEIXE:
B)A SENTENÇA Q PERMITE CALCULAR O GASTO MENSAL(G), EM REAIS, EM FUNÇÃO DA QUANTIDADE DE PEIXE (P) EM KG COMPRADA NO MES.
obs: TENTEI ENTENDER ESSA QUESTÃO ATRAVÉS DE UM SISTEMA DE EQUAÇÃO DO 1º GRAU, MAS NÃO FOI POSSÍVEL JÁ QUE A PERGUNTA DA LETRA A) PARECE DESCARTAR A POSSIBILIDADE DE USARMOS A CARNE. DESDE JÁ AGRADEÇO A ATENÇÃO DOS AMIGOS DESTA PÁGINA.
-
rcpn
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Abr 08, 2014 10:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: formação geral
- Andamento: formado
 por Russman » Qua Abr 09, 2014 00:12
por Russman » Qua Abr 09, 2014 00:12
Façamos
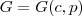
. A função
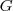
é o gasto total mensal da compra de

kilogramas de peixe e

kilogramas de carne.
Do enunciado,
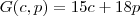
. Concorda?
Se sim, note ainda que a quantidade de kilogramas TOTAL de carne e peixe deve ser de 30 kg. Assim, para qualquer gasto
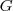
é preciso que
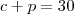
. Daí,
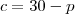
e a função passa a depender somente explicitamente de

.
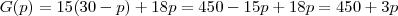
.
Se foram comprados 10 kg de peixe, então o gasto foi de
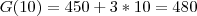
.
Veja que se foram comprados 10 kg de peixe então , necessariamente, a quantidade de carne foi de 20 kg. Esses números podem ser substituídos em
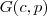
e você encontrará o mesmo valor.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Matemático
por honorio » Dom Set 06, 2009 20:06
- 10 Respostas
- 7705 Exibições
- Última mensagem por honorio

Dom Set 20, 2009 17:25
Funções
-
- Problema matemático
por thiagocsouza » Ter Jan 03, 2012 22:41
- 8 Respostas
- 5051 Exibições
- Última mensagem por Arkanus Darondra

Sáb Jan 07, 2012 22:12
Sistemas de Equações
-
- Problema matematico
por girotto » Seg Jun 11, 2012 16:34
- 1 Respostas
- 1692 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 18:50
Sistemas de Equações
-
- problema matemático de vendas
por vb_evan » Sáb Mar 06, 2010 15:20
- 2 Respostas
- 3037 Exibições
- Última mensagem por vb_evan

Dom Mar 07, 2010 09:16
Dúvidas Pendentes (aguardando novos colaboradores)
-
- duvida em um problema matematico
por diogo_poa » Ter Mar 23, 2010 23:15
- 0 Respostas
- 1360 Exibições
- Última mensagem por diogo_poa

Ter Mar 23, 2010 23:15
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


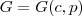 . A função
. A função 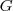 é o gasto total mensal da compra de
é o gasto total mensal da compra de  kilogramas de peixe e
kilogramas de peixe e  kilogramas de carne.
kilogramas de carne.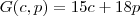 . Concorda?
. Concorda?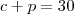 . Daí,
. Daí, 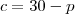 e a função passa a depender somente explicitamente de
e a função passa a depender somente explicitamente de 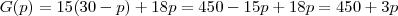 .
.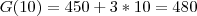 .
.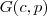 e você encontrará o mesmo valor.
e você encontrará o mesmo valor.