Gostaria de ajuda para resolver, não sei como fazer.
(UFRN)A figura abaixo é composta por dois eixos perpendiculares entre si, X e Y, que se intersectam no centro O de um círculo de raio 1, e outro eixo Z, paralelo a Y e tangente ao círculo no ponto P. A semi-reta OQ, com Q pertencente a Z, forma um ângulo a com o eixo Y. Podemos afirmar que o valor da medida do segmento PQ é:
a)sec ?
b)tg ?
c)cotg ?
d)cos ?
Gabarito: letra C
Obrigada.


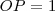 e
e 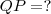 e hipotenusa
e hipotenusa 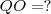 .Ora ,se por hipótese "A semi-reta OQ, com Q pertencente a Z, forma um ângulo
.Ora ,se por hipótese "A semi-reta OQ, com Q pertencente a Z, forma um ângulo  com o eixo Y" , então A semi-reta QP, com Q pertencente a Z , também forma um ângulo
com o eixo Y" , então A semi-reta QP, com Q pertencente a Z , também forma um ângulo  . Substituindo na fórmula ,obterá o resultado .
. Substituindo na fórmula ,obterá o resultado .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.