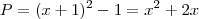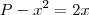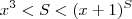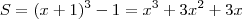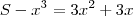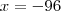por BrenoNaval » Dom Mar 30, 2014 19:27
por BrenoNaval » Dom Mar 30, 2014 19:27
A raiz quadrada de um número P é igual a x e o resto é o maior possível.A raiz cúbica de um número S é igual a x e o resto também é o maior possível.Se a soma desses restos é 288,qual é a soma dos dígitos do número S?
Resposta: 27
Esse exercício foi retirado do livro Praticando Aritmética do capítulo de Radiciação.
Para facilitar o entendimento,de primeira mão irei informar a vocês alguns dados a parte.
Teorema 1: ''O maior resto que se pode encontrar na extração da raiz quadrada de um número natural N é igual ao dobro da raiz.''
Ex.:Tome A=8 ,o maior quadrado perfeito em 8=>4=2²
Logo o maior resto=3²-1-2²=2.2
Teorema 2:''O maior resto que se pode encontrar no extração da raiz cúbica de um número N é igual ao triplo do quadrado da raiz mais o triplo da raiz.''
ex.:Tome S=26=3³-1 ,o maior cubo perfeito em 26=>8=2³
Logo o maior resto=3³-1-2³=3.2²+3.2
Tentei utilizar esses dados na questão mais resultou em uma equação muito complexa. Resposta da questão:27
-
BrenoNaval
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 30, 2014 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mar 30, 2014 19:36
por Russman » Dom Mar 30, 2014 19:36
De que livro são esses Teoremas?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por BrenoNaval » Dom Mar 30, 2014 19:40
por BrenoNaval » Dom Mar 30, 2014 19:40
praticando a aritmética josé carlos admo lacerda-Capítulo de radiciação
-
BrenoNaval
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 30, 2014 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Seg Mar 31, 2014 18:20
por young_jedi » Seg Mar 31, 2014 18:20
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por BrenoNaval » Sex Abr 11, 2014 12:02
por BrenoNaval » Sex Abr 11, 2014 12:02
Resposta correta.
Eu cheguei a ter esse pensamento,no entanto pelo motivo de o livro na qual eu estou resolvendo(praticando aritmética) ter apenas a formula 2x e 3y²+3y eu não cheguei a conclusão de que x²<p<(x+1)² ou que Y³<P<(Y+1)³,no caso dessa questão especifica que que X e Y serão iguais.
Contudo, muito Obrigado por sua ajuda.
-
BrenoNaval
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 30, 2014 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Algum gênio consegue resolver isso? Álgebra elementar
por BrenoNaval » Dom Abr 13, 2014 22:06
- 1 Respostas
- 3142 Exibições
- Última mensagem por e8group

Seg Abr 14, 2014 01:33
Álgebra Elementar
-
- algum me ajuda
por danielfonteles » Seg Abr 17, 2017 18:07
- 0 Respostas
- 1180 Exibições
- Última mensagem por danielfonteles

Seg Abr 17, 2017 18:07
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Desconto algum me ajuda por favor
por tr105385 » Qui Jul 30, 2009 14:00
- 3 Respostas
- 2048 Exibições
- Última mensagem por tr105385

Qui Jul 30, 2009 19:25
Estatística
-
- Obter o comando LaTeX para algum símbolo
por LuizAquino » Seg Abr 11, 2011 19:24
- 1 Respostas
- 5785 Exibições
- Última mensagem por Neperiano

Sex Out 21, 2011 16:28
Sites Recomendados / Outras Indicações
-
- Função inversa [Gabarito não fecha de jeito algúm]
por Matheus Lacombe O » Qui Set 06, 2012 00:37
- 3 Respostas
- 2578 Exibições
- Última mensagem por MarceloFantini

Qui Set 06, 2012 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.