 por Rafael Zanelato » Seg Mar 31, 2014 14:17
por Rafael Zanelato » Seg Mar 31, 2014 14:17
Estou no primeiro semestre de engenharia civil e estou com dificuldades nesse exercício.
Agradeço desde já!
- Anexos
-
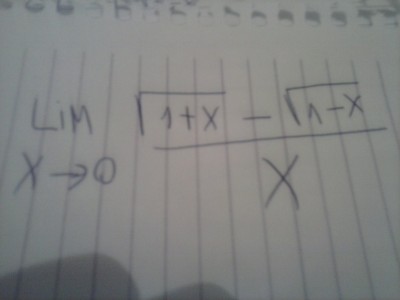
-
Rafael Zanelato
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Cleyson007 » Seg Mar 31, 2014 14:29
por Cleyson007 » Seg Mar 31, 2014 14:29
Boa tarde Rafael!
Repare que se você substituir o 0 no numerador e no denominador terá uma indeterminação do tipo 0

. Para que não ocorra a indeterminação, multiplique o numerador e o denominador por
![\sqrt[]{1+x}+\,\sqrt[]{1-x} \sqrt[]{1+x}+\,\sqrt[]{1-x}](/latexrender/pictures/cb67d53382015a30efe8fe6f0058fad1.png)
.
Qualquer dúvida estou a disposição.
Abraço,
Cleyson
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Rafael Zanelato » Seg Mar 31, 2014 16:09
por Rafael Zanelato » Seg Mar 31, 2014 16:09
Boa tarde,
Até ai eu sei chegar, mas eu travo durante essa multiplicação.
Se alguém puder me mandar toda a resolução ficaria grato.
Att,
Rafael Zanelato
-
Rafael Zanelato
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Man Utd » Ter Abr 01, 2014 11:28
por Man Utd » Ter Abr 01, 2014 11:28
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Sex Out 23, 2009 20:36
- 1 Respostas
- 2425 Exibições
- Última mensagem por Tom

Sáb Jul 03, 2010 21:30
Sequências
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Qua Out 28, 2009 23:47
- 0 Respostas
- 1388 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite modular, me ajudem!
por arthurvct » Ter Abr 23, 2013 14:50
- 3 Respostas
- 1523 Exibições
- Última mensagem por arthurvct

Ter Abr 23, 2013 17:18
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Por favor ajudem
por michelcosta » Dom Nov 17, 2013 10:11
- 0 Respostas
- 531 Exibições
- Última mensagem por michelcosta

Dom Nov 17, 2013 10:11
Cálculo: Limites, Derivadas e Integrais
-
- me ajudem neste exercício de limite
por Claudia Sotero » Sex Nov 20, 2009 16:15
- 2 Respostas
- 4225 Exibições
- Última mensagem por Claudia Sotero

Sáb Nov 21, 2009 10:47
Computação
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Para que não ocorra a indeterminação, multiplique o numerador e o denominador por
. Para que não ocorra a indeterminação, multiplique o numerador e o denominador por ![\sqrt[]{1+x}+\,\sqrt[]{1-x} \sqrt[]{1+x}+\,\sqrt[]{1-x}](/latexrender/pictures/cb67d53382015a30efe8fe6f0058fad1.png) .
.

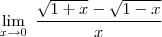
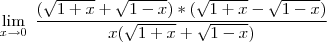
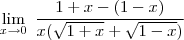
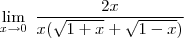
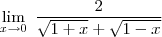

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)