 por Elcioschin » Seg Dez 07, 2009 22:45
por Elcioschin » Seg Dez 07, 2009 22:45
Gabriela
Acho que vc não entendeu o que eu escreví quando eu au falei a respeito de resposta:
O que eu disse foi o seguinte; Quando você tiver uma dúvida e postá-la no forum, caso você já conheça o resultado (o gabarito da questão), coloque por favor junto com o enunciado, para facilitar a vida de quem pretende ajudá-la.
Por exemplo, caso vc já soubesse que o resultado era 792 deveria tê-lo colocado junto com o enunciado. Até agora eu não sei se a minha solução está correta, pois vc não comentou nada a respeito.
Quanto ao fato de "eu ter ido direto" na questão, não existe outro caminho para chegar nela: O meu caminho, idêntico ao do Cleyson, resumiu-se SIMPLESMENTE na aplicação da única fórmula BÁSICA existente sobre combinações.
Infelizmente parece que vc não conhece esta fórmula básica, já que vc não entendeu a minha solução. Esta foi a razão do meu conselho para vc se esforçar e ESTUDAR o assunto de forma a aprender a usar a fórmula.
Acho que vc também não entendeu o significado sobre as regras de interação do forum:
Vc simplesmente colocou o enunciado e não mostrou suas tentativas de resolver o problema, para que pudéssemos entender qual era a sua dificuldade. Vc disse apenas "já fiz de todo jeito e não consegui". Que jeitos foram esses?
Logo, vc não interagiu!
E reitero o meu conselho: Estude!







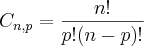





 .
.
 :
: