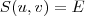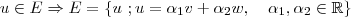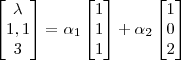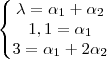MAT0134
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Cicero ferreira » Sex Mar 14, 2014 18:23
por Cicero ferreira » Sex Mar 14, 2014 18:23
Determinar o valor de

para que o vetor
![u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right] u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right]](/latexrender/pictures/d6ac7d35123251037f60dede223bc6b8.png)
pertença ao subespaço gerado pelos vetores
![v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right]. v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right].](/latexrender/pictures/20e5e4bc91012ba3daf5efd9849fbb2a.png)
-
Cicero ferreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 04, 2014 13:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Russman » Sex Mar 14, 2014 23:00
por Russman » Sex Mar 14, 2014 23:00
O subespaço gerado pelos vetores
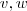
, seja ele

, é tal que se um vetor

pertence a

então

é escrito como combinação linear de

e
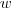
. Ou seja,
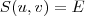
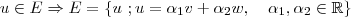
Assim, temos
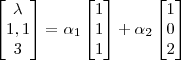
Ou,
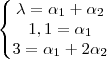
Agora resolva o sistema, isto é, calcule os valores dos alphas ( na verdade só de alpha_2, pois alpha_1 já está especificado o valor), some-os e terá o valor de lambda.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Introdução à Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Subespaço gerado
por drleonunes » Qui Abr 16, 2015 21:10
- 0 Respostas
- 1522 Exibições
- Última mensagem por drleonunes

Qui Abr 16, 2015 21:10
Álgebra Linear
-
- Vetores LI e LD - Subespaço Gerado
por Cicero ferreira » Sex Mar 14, 2014 18:13
- 0 Respostas
- 2049 Exibições
- Última mensagem por Cicero ferreira

Sex Mar 14, 2014 18:13
Álgebra I para Licenciatura
-
- Álgebra linear - Subespaço Gerado
por nietzsche » Sex Jan 06, 2012 19:48
- 2 Respostas
- 1913 Exibições
- Última mensagem por nietzsche

Ter Jan 10, 2012 17:16
Álgebra Linear
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10987 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4683 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para que o vetor
para que o vetor ![u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right] u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right]](/latexrender/pictures/d6ac7d35123251037f60dede223bc6b8.png) pertença ao subespaço gerado pelos vetores
pertença ao subespaço gerado pelos vetores![v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right]. v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right].](/latexrender/pictures/20e5e4bc91012ba3daf5efd9849fbb2a.png)

 para que o vetor
para que o vetor ![u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right] u = \left[ \begin{array}{ccc} \lambda\\ 1,1\\3\\ \end{array} \right]](/latexrender/pictures/d6ac7d35123251037f60dede223bc6b8.png) pertença ao subespaço gerado pelos vetores
pertença ao subespaço gerado pelos vetores![v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right]. v = \left[ \begin{array}{ccc} 1\\ 1\\1\\ \end{array} \right]
w = \left[ \begin{array}{ccc} 1\\ 0\\2\\ \end{array} \right].](/latexrender/pictures/20e5e4bc91012ba3daf5efd9849fbb2a.png)

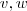 , seja ele
, seja ele  , é tal que se um vetor
, é tal que se um vetor  pertence a
pertence a  então
então  é escrito como combinação linear de
é escrito como combinação linear de  e
e 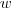 . Ou seja,
. Ou seja,