 por Ana Maria da Silva » Sáb Mar 01, 2014 23:05
por Ana Maria da Silva » Sáb Mar 01, 2014 23:05
Como faço pra desenvolver ?
O Domínio da função
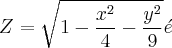
a- Um disco aberto de raio 36.
b. O interior de um retângulo.
c. O exterior de um retângulo.
d. O interior de uma elipse.
e. A região fechada exterior a uma elipse.
f. O exterior de uma elipse.
g. A região compacta delimitada por uma elipse.
-
Ana Maria da Silva
- Usuário Parceiro

-
- Mensagens: 83
- Registrado em: Qua Mar 27, 2013 15:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Gregorio Diniz » Qua Mar 12, 2014 18:19
por Gregorio Diniz » Qua Mar 12, 2014 18:19
Nesta questão devemos primeiro perceber que a expressão dentro da raiz não pode ser menor que zero.
Tendo isso em vista,
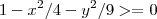
, logo
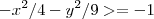
. Multiplicando tudo por (-1), temos:
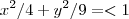
.
E essa última expressão indica exatamente a região de uma elipse e o seu interior, de eixo maior 6 e eixo menor 4.
Abraço
-
Gregorio Diniz
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 08, 2014 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3249 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2885 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1770 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5164 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
-
- Domínio de uma função
por Jonatan » Qui Jul 29, 2010 15:46
- 0 Respostas
- 1862 Exibições
- Última mensagem por Jonatan

Qui Jul 29, 2010 15:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
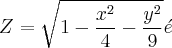


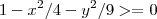 , logo
, logo 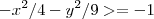 . Multiplicando tudo por (-1), temos:
. Multiplicando tudo por (-1), temos: 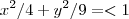 .
.
