
http://img694.imageshack.us/i/revisao.jpg/ (Questão link)
Não entendi como achar tal área.
Obrigado, abraços!






 .
. bastava integrar
bastava integrar  . Porém, perceba que eu quero a área embaixo da reta, porém, tirando a parte da área da parábola dada por
. Porém, perceba que eu quero a área embaixo da reta, porém, tirando a parte da área da parábola dada por  . Note ainda que a área que queremos está entre os pontos -2 e -1. Logo, esses serão os limites da integral:
. Note ainda que a área que queremos está entre os pontos -2 e -1. Logo, esses serão os limites da integral:

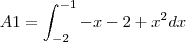

![A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1} A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1}](/latexrender/pictures/3bb58e6f1e736cd9b2d4b3ba9bebb999.png)




igones escreveu:Muito obrigado, cosnegui entender.
Mas, não entendi esse intervalo (-2, -1), não to vendo ele na figura =/
Explica essa parte por favor
Obrigado!
Abraços!



igones escreveu:Consegui sim!
São 3 regioes sombreadas neh?!
Eu só tava vendo 2..
Então vc calculou a área de cada região e depois somou as 3 que da a area total certo?
Obrigado! =D







Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.