![\lim_{x\rightarrow\infty} \frac{3x^5+2x-8}{\sqrt[2]{x^6+x+1}} \lim_{x\rightarrow\infty} \frac{3x^5+2x-8}{\sqrt[2]{x^6+x+1}}](/latexrender/pictures/d591184d4f2ef9ea71ed87ccd664ae06.png)
resp.:

Ao tentar resolvê-lo, multipliquei o numerador e o denominador por (1/(x^3)). No denominador obtive, dentro da raíz, 1+1/x^5 + 1/x^6(e com x tendendo a menos infinito, sobrou 1). No numerador, 3x^2 + 2/(x^2) - 8/(x^3), e com x tendendo à menos infinito, sobra 3*(-inf)^2, o que eu imaginei, daria +infinito. Mas a resposta é - infinito !. Alguém sabe como chegar nisso ?


![\lim_{x\rightarrow -\infty} \frac{3x^5+2x-8}{\sqrt[2]{x^6+x+1}} \lim_{x\rightarrow -\infty} \frac{3x^5+2x-8}{\sqrt[2]{x^6+x+1}}](/latexrender/pictures/e5b375807885a3cc72bde7b46922727e.png)

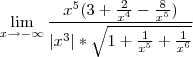
 e sim
e sim  .e veja tbm que :
.e veja tbm que : 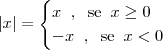 , como o limite tende a valores muito grandes e negativos ficamos com:
, como o limite tende a valores muito grandes e negativos ficamos com:

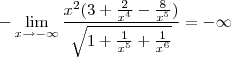



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)