Imagino que o enunciado seja:
"A razão entre o lado do triângulo equilátero inscrito e o lado do triângulo equilátero circunscrito em uma circunferência de raio R é:"
Primeiro, lembremos que no caso do triângulo equilátero, o baricentro do triângulo inscrito e o do circunscrito coincidem com o seu centro.
Segundo, lembremos que o baricentro divide cada mediana na razão de 2 para 1. A distância entre o vértice e o baricentro é o dobro da distância entre o baricentro e a base.
Vamos á resolução:

, e como,
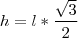
,após substituir h, e desenvolver, obtemos
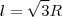
.
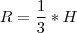
, e como,

,após substituir H, e desenvolver, obtemos

.
Portanto,

.
Valeu!!! Bom retiro pra quem é de retiro!!!Bom carnaval pra quem é de carnaval!!!



 , e como,
, e como, 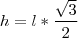 ,após substituir h, e desenvolver, obtemos
,após substituir h, e desenvolver, obtemos 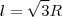 .
.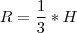 , e como,
, e como,  ,após substituir H, e desenvolver, obtemos
,após substituir H, e desenvolver, obtemos  .
. .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

