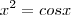


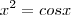



brunnkpol escreveu:Obrigado pela sugestão. Usando o método de newton, achei o valor, mas apenas o positivo. O gráfico (pelo programa de computador) mostra que as funções se interceptam no mesmo valor tanto negativo quanto positivo de x
 , um valor aproximado para a raiz positiva da eq. dada , ent'ao
, um valor aproximado para a raiz positiva da eq. dada , ent'ao 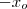 eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.
eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.brunnkpol escreveu:Outra dúvida é se existe algum meio que eu possa descobrir simplesmente em quantos pontos uma função intercepta a outra.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.