 por Giudav » Ter Fev 11, 2014 18:00
por Giudav » Ter Fev 11, 2014 18:00
(Uece) Sejam A = {2,4,6,8,10,12...64} e B = {(m,n)

A x A / m+n = 64}. O número de elementos de B é iqual a:
a)31
b)32
c)62
d)64
Resolução minha: se A vai até 64 .:. temos 32 elementos aplicando aqui ''A x A / m+n = 64}'' 1024/64 = m ou n =16 .:. 16+16=32 (b)
Gabarito (a)
-
Giudav
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Fev 21, 2012 23:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Fev 11, 2014 18:48
por e8group » Ter Fev 11, 2014 18:48
Você contou um a mais .Pois se

então
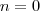
e
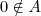
.Logo ,

.Outra forma de escrever o conjunto

:

.
Se
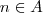
e

, então o número

positivo é par e é menor que 64 ; pelo que este número tbm está no conjunto

. Logo , o par ordenado
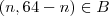
desde que
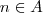
e

.Isto justifica que

possui 31 elementos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão da UECE
por Kelvin Brayan » Dom Mar 27, 2011 13:26
- 9 Respostas
- 10604 Exibições
- Última mensagem por Kelvin Brayan

Dom Mar 27, 2011 17:02
Funções
-
- Piramide UECE
por Maria Livia » Sex Nov 16, 2012 11:45
- 1 Respostas
- 9391 Exibições
- Última mensagem por young_jedi

Sex Nov 16, 2012 12:23
Geometria Espacial
-
- Logarítmos UECE
por Amanda185 » Qua Mai 22, 2013 15:37
- 2 Respostas
- 5989 Exibições
- Última mensagem por nicholasrr

Qui Abr 03, 2014 21:30
Logaritmos
-
- Questão da UECE
por vini15963 » Seg Set 22, 2014 01:25
- 0 Respostas
- 3601 Exibições
- Última mensagem por vini15963

Seg Set 22, 2014 01:25
Geometria Espacial
-
- Questão UECE 2012
por Phaniemor » Qui Abr 18, 2013 11:33
- 1 Respostas
- 4475 Exibições
- Última mensagem por DanielFerreira

Qui Abr 18, 2013 12:01
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 A x A / m+n = 64}. O número de elementos de B é iqual a:
A x A / m+n = 64}. O número de elementos de B é iqual a:
 A x A / m+n = 64}. O número de elementos de B é iqual a:
A x A / m+n = 64}. O número de elementos de B é iqual a:
 então
então 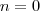 e
e 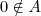 .Logo ,
.Logo ,  .Outra forma de escrever o conjunto
.Outra forma de escrever o conjunto  :
:  .
.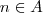 e
e  , então o número
, então o número  positivo é par e é menor que 64 ; pelo que este número tbm está no conjunto
positivo é par e é menor que 64 ; pelo que este número tbm está no conjunto  . Logo , o par ordenado
. Logo , o par ordenado 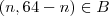 desde que
desde que 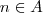 e
e  .Isto justifica que
.Isto justifica que  possui 31 elementos .
possui 31 elementos .
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
