
R:2
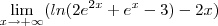
R:ln2


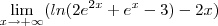

 para todo
para todo  .
.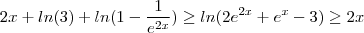 .
. para
para  , obtemos
, obtemos  .
. e em seguida utilizar a propriedade
e em seguida utilizar a propriedade  .
. 
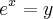 , mas não consegui chegar ao resultado.
, mas não consegui chegar ao resultado.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes

 .
.
 :
: