
Resposta: -1



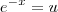 . Agora tente concluir .
. Agora tente concluir .
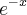 por y:
por y:


 , então
, então  e além disso ,
e além disso , ![ln(e^{-x} -1) = ln(y-1) = ln \left(y \left[1 - \dfrac{1}{y}\right]\right) = ln(y) + ln(1 - \dfrac{1}{y}) ln(e^{-x} -1) = ln(y-1) = ln \left(y \left[1 - \dfrac{1}{y}\right]\right) = ln(y) + ln(1 - \dfrac{1}{y})](/latexrender/pictures/3b36f1f06f71cc35cb0467472330e987.png) (pois como definimos
(pois como definimos  , ele sempre será > 0 ) .
, ele sempre será > 0 ) . 
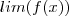 significa
significa 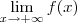 e ao invés de dizermos a função f contínua ou de classe C^0 , definida por f(x) , vamos dizer apenas f(x) é contínua )
e ao invés de dizermos a função f contínua ou de classe C^0 , definida por f(x) , vamos dizer apenas f(x) é contínua )  e
e  implicam
implicam 
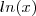 é contínua em 1 e
é contínua em 1 e 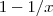 é descontínua apenas na origem . Logo ,a segunda função é contínua em valores arbitrariamente grandes e
é descontínua apenas na origem . Logo ,a segunda função é contínua em valores arbitrariamente grandes e 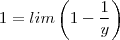 .Portanto
.Portanto ![lim\left(ln\left[1 - \frac{1}{y}\right]\right) = ln\left(lim\left[1 - \frac{1}{y}\right] \right)= ln(1) = 0 lim\left(ln\left[1 - \frac{1}{y}\right]\right) = ln\left(lim\left[1 - \frac{1}{y}\right] \right)= ln(1) = 0](/latexrender/pictures/1853f56e3a0f8849164dc677fc589fc4.png) .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes

 .
.
 :
: