 por magellanicLMC » Sáb Fev 08, 2014 17:35
por magellanicLMC » Sáb Fev 08, 2014 17:35
eu n pude especificar um assunto pqe n sei qual integral é essa se alguém pudesse me dar uma ajuda nisso
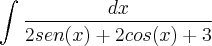
eu não sei nem por onde começar...
-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Man Utd » Qui Fev 13, 2014 17:50
por Man Utd » Qui Fev 13, 2014 17:50
magellanicLMC escreveu:eu n pude especificar um assunto pqe n sei qual integral é essa se alguém pudesse me dar uma ajuda nisso
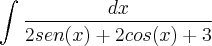
eu não sei nem por onde começar...
Veja que :
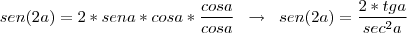
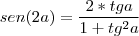
faça
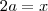
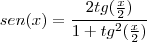
sabendo que
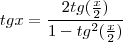
chegamos a
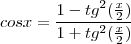
, substitua na integral:
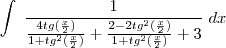
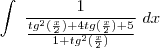
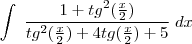
façamos a subsittuição
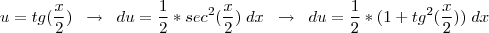
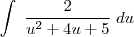
consegue avançar?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4609 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4574 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4340 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2838 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2861 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
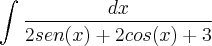 eu não sei nem por onde começar...
eu não sei nem por onde começar...

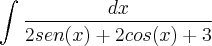 eu não sei nem por onde começar...
eu não sei nem por onde começar...
eu não sei nem por onde começar...
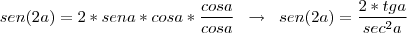
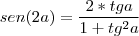
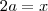
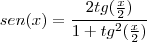
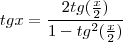 chegamos a
chegamos a 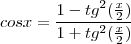 , substitua na integral:
, substitua na integral: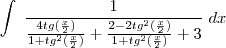
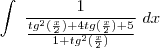
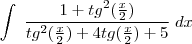
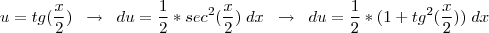
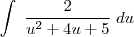

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
