seja
![f(x)=3\sqrt[2]{x+1} f(x)=3\sqrt[2]{x+1}](/latexrender/pictures/2625da596fd73d48764db0e128d90dbc.png) encontre o valor médio no intervalo [-1,3]
encontre o valor médio no intervalo [-1,3]![3\int_{-1}^{3}\sqrt[2]{x+1}dx 3\int_{-1}^{3}\sqrt[2]{x+1}dx](/latexrender/pictures/fb67a1cacaaa57a200be58e5b483a9a1.png)
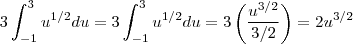
calculando dentro dos limites fica 16
como valor médio é dentro do intervalo fica
 , que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
, que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
![f(x)=3\sqrt[2]{x+1} f(x)=3\sqrt[2]{x+1}](/latexrender/pictures/2625da596fd73d48764db0e128d90dbc.png) encontre o valor médio no intervalo [-1,3]
encontre o valor médio no intervalo [-1,3]![3\int_{-1}^{3}\sqrt[2]{x+1}dx 3\int_{-1}^{3}\sqrt[2]{x+1}dx](/latexrender/pictures/fb67a1cacaaa57a200be58e5b483a9a1.png)
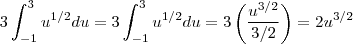
 , que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
, que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)