 por Jhenrique » Sex Jan 31, 2014 18:55
por Jhenrique » Sex Jan 31, 2014 18:55
Como eu faço para derivar um vetor unitário? Aliás, como esse assunto se encaixa com os símbolos de christoffel, com derivadas parciais versus totais de vetores untitários... enfim, qual é o passo a passo para derivar um vetor unitário? Qual a fórmulas geral, qual a regra?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Sáb Fev 01, 2014 00:48
por Russman » Sáb Fev 01, 2014 00:48
Vetor unitário, por definição, tem módulo igual a 1. Assim, basta você derivar apenas o direção e o sentido, já que a derivada do módulo é nula.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sáb Fev 01, 2014 01:04
por Jhenrique » Sáb Fev 01, 2014 01:04
na prática, como fica a equação?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Sáb Fev 01, 2014 02:26
por Russman » Sáb Fev 01, 2014 02:26
Depende de como você expressará os vetores, logicamente. Comece com
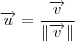
especificando a base de
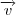
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sáb Fev 01, 2014 08:26
por Jhenrique » Sáb Fev 01, 2014 08:26
Han? Eu não entendi exatamente o que significa especificar a base...
Contudo, há uma outra questão muito relevante que até agora eu não entendi...
segundo o wolfram
http://mathworld.wolfram.com/Cylindrica ... nates.htmlA derivada do vetor unitário r com relação a váriavel teta é
d
r/d? =
?Mas pelo símbolos de christoffel que constam lá a derivada fica como:
d
r/d? = 1/r
?O que não pode ser verdade, uma dessas duas equações acima tem que estar errada, ou não, não sei. Como que eu uso os símbolos de christoffel corretamente?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dirvergência e rotacional de vetores unitários
por Jhenrique » Sáb Fev 01, 2014 09:54
- 0 Respostas
- 989 Exibições
- Última mensagem por Jhenrique

Sáb Fev 01, 2014 09:54
Geometria Analítica
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7364 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2988 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5210 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3402 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





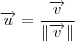
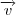 .
.

