 por e8group » Seg Jan 20, 2014 23:45
por e8group » Seg Jan 20, 2014 23:45
Boa noite . Preciso mostrar que toda sequência periódica e convergente é constante . Por favor ,avaliem minha solução , dicas são bem vindas .
Sol.:
Dada a sequência
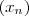
periódica e convergente ,
poremos

.Em virtude da periodicidade da sequência ,existe
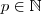
tal que
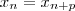
para todo

natural .Mas ,novamente por periodicidade ,temos
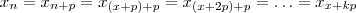
para quaisquer que seja
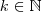
.Daí , quando

for suficientemente grande o termo
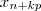
converge para

,e assim
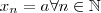
o que assegura
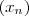
é constante.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- IME-96 Função periódica
por Balanar » Sáb Ago 07, 2010 17:58
- 4 Respostas
- 10890 Exibições
- Última mensagem por kamillanjb

Ter Mar 15, 2011 22:57
Desafios Difíceis
-
- P.G. Dízima Periódica
por Rafael16 » Qua Jul 18, 2012 19:48
- 3 Respostas
- 8153 Exibições
- Última mensagem por Russman

Qua Jul 18, 2012 21:20
Progressões
-
- Dizima periodica composta
por creberson » Sex Mai 24, 2019 11:03
- 1 Respostas
- 9628 Exibições
- Última mensagem por DanielFerreira

Qui Set 12, 2019 23:19
Conjuntos
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3995 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- CONVERGENTE
por camilasereno » Sáb Jun 11, 2016 20:30
- 0 Respostas
- 3652 Exibições
- Última mensagem por camilasereno

Sáb Jun 11, 2016 20:30
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
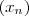 periódica e convergente ,
periódica e convergente , .Em virtude da periodicidade da sequência ,existe
.Em virtude da periodicidade da sequência ,existe 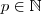 tal que
tal que 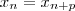 para todo
para todo  natural .Mas ,novamente por periodicidade ,temos
natural .Mas ,novamente por periodicidade ,temos 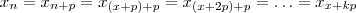 para quaisquer que seja
para quaisquer que seja 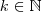 .Daí , quando
.Daí , quando  for suficientemente grande o termo
for suficientemente grande o termo 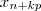 converge para
converge para  ,e assim
,e assim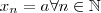 o que assegura
o que assegura 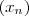 é constante.
é constante.

