Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Luiz Augusto Prado » Sex Nov 27, 2009 19:23
por Luiz Augusto Prado » Sex Nov 27, 2009 19:23
Olá Pessoa!
Estou começando a colecionar questões que possam ferrar alunos. Sendo assim, gostaria de uma ajuda de vcs. Tenho uma questão: Quero saber todas as formas possíveis para a solução desta indeterminação:
![\lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}}](/latexrender/pictures/6cb7b0b9898bd1a29405699072c2dbb9.png)
-

Luiz Augusto Prado
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Nov 27, 2009 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Elcioschin » Sáb Nov 28, 2009 18:19
por Elcioschin » Sáb Nov 28, 2009 18:19
Neste caso é muito simples
V(x - 2)/V(x² - 4) = V(x - 2)/V[(x - 2)*(x + 2)] = [V(x - 2)/V(x - 2)]*[1/V(x + 2)] = 1/V(x + 2)
Para x = 2 ----> 1/V(4) = 1/2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Luiz Augusto Prado » Sáb Nov 28, 2009 21:13
por Luiz Augusto Prado » Sáb Nov 28, 2009 21:13
Acho que este limite é -infinito quando x tende a 2 pela direita.
veja que o denominador é uma raiz cubica.
eu coloquei estes radicais diferentes porque quero obrigar o estudante a mudar a formula antes de usar L'Hopital. Isso se ele quiser usar L'Hopital, pois não é obrigatório.
-

Luiz Augusto Prado
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Nov 27, 2009 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Elcioschin » Dom Nov 29, 2009 11:15
por Elcioschin » Dom Nov 29, 2009 11:15
Luiz
Desculpe o meu engano: eu não tinha visto que era raiz cúbica no denominador.
²V(x - 2)/³V(x² - 4) = ²V(x - 2)/³V[(x - 2)*(x + 2)] = ²V(x - 2)/[³V(x - 2)]*[³V(x + 2)] =
= (x - 2)^(1/2)/[(x - 2)^(1/3)]*[(x + 2)^(1/3)] = [(x - 2)^(1/2 - 1/3)/(x + 2)^(1/3) = (x - 2)^(1/6)/(x + 2)^(1/3)
Aplicando limite para x = 2 -----> 0/4^(1/3) = 0
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Luiz Augusto Prado » Seg Nov 30, 2009 11:20
por Luiz Augusto Prado » Seg Nov 30, 2009 11:20
vc escreveu:
²V(x - 2)/³V(x² - 4) = ²V(x - 2)/³V[(x - 2)*(x + 2)] = ²V(x - 2)/[³V(x - 2)]*[³V(x + 2)] =
![\frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0 \frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0](/latexrender/pictures/e3cfc1351020cd8a7d8c29afd4ad4a78.png)
Muito boa sua solução!
Tentei por outro modo aplicando L'Hopital assim:
![\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)}](/latexrender/pictures/fd56810d8924cc94867f3e9285aeaa00.png)
Onde meu limite passaria a depender de:

Onde apliquei L'Hopital duas vezes:
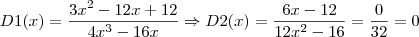
Se existe um resultado para um valor que tende a zero pela direita em ln(0), este valor é -infinito.
Outra forma:
![\sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} } \sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} }](/latexrender/pictures/b0b8935e4f09b504eeb72fb27711db61.png)
-

Luiz Augusto Prado
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Nov 27, 2009 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}}](/latexrender/pictures/6cb7b0b9898bd1a29405699072c2dbb9.png)

![\lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}}](/latexrender/pictures/6cb7b0b9898bd1a29405699072c2dbb9.png)




![\frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0 \frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0](/latexrender/pictures/e3cfc1351020cd8a7d8c29afd4ad4a78.png)
![\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)}](/latexrender/pictures/fd56810d8924cc94867f3e9285aeaa00.png)

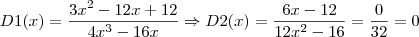
![\sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} } \sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} }](/latexrender/pictures/b0b8935e4f09b504eeb72fb27711db61.png)


 .
.
 :
: