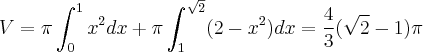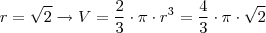por Pessoa Estranha » Dom Jan 12, 2014 16:15
por Pessoa Estranha » Dom Jan 12, 2014 16:15
Olá, pessoal! Estou com problemas no seguinte exercício:
"CALCULE O VOLUME DO SÓLIDO OBTIDO PELA ROTAÇÃO, EM TORNO DO EIXO X, DO CONJUNTO DE TODOS OS PARES (X,Y) TAIS QUE:
H)
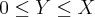
E
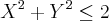
."
Minha resolução:
![\int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3} \int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3}](/latexrender/pictures/9008b58d7cd94393af47295d66ee8bcc.png)
Está errado. Por que?
Obrigada! (Pessoal, é urgente!)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Ter Jan 14, 2014 09:07
por Pessoa Estranha » Ter Jan 14, 2014 09:07
A sua resolução está certa, mas por que a minha não deu certo?
Obrigada por responder!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Guilherme Pimentel » Qua Jan 15, 2014 04:48
por Guilherme Pimentel » Qua Jan 15, 2014 04:48
Vc considerou que toda a função a ser integrada era a circunferencia, ignorou a parte que é reta. Dito de outra forma, vc calculou o volume de um hemisferio de raio
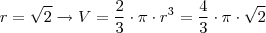
-
Guilherme Pimentel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Dom Jan 12, 2014 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Economia
- Andamento: formado
 por Pessoa Estranha » Qua Jan 15, 2014 09:13
por Pessoa Estranha » Qua Jan 15, 2014 09:13
Entendi! Obrigada!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4527 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3678 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Cálculo de integral
por LAZAROTTI » Dom Set 30, 2012 19:52
- 0 Respostas
- 1194 Exibições
- Última mensagem por LAZAROTTI

Dom Set 30, 2012 19:52
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3270 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3160 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
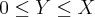 E
E 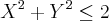 ."
."![\int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3} \int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3}](/latexrender/pictures/9008b58d7cd94393af47295d66ee8bcc.png)

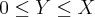 E
E 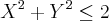 ."
."![\int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3} \int_{0}^{\sqrt[]{2}} \pi (2-{x}^{2})dx = 2.\sqrt[]{2}\pi - \frac{2.\sqrt[]{2}\pi}{3} = \frac{4.\sqrt[]{2}\pi}{3}](/latexrender/pictures/9008b58d7cd94393af47295d66ee8bcc.png)