Considere a função s = t³ + 3t² - 9t + 4 como sendo a função-movimento de uma partícula ao longo de uma reta horizontal (com sentido positivo à direita).
1. Determine os intervalos de tempo em que a partícula move-se para a direita e para a esquerda.
2. Determine quando a partícula reverte o sentido do movimento.
3. Esboce o comportamento do movimento através de um gráfico.
Agradeço quem puder ajudar
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bom, na verdade minhas dúvidas são teóricas..
Sei que a partícula se move para a direita quando v(t) > 0.
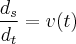
Escrevendo a equação de forma fatorada: v(t) = 3(t - 1)(t + 3)
Para que v(t) > 0: t > 1 ou t > -3
Alguém pode me explicar de maneira detalhada?
No aguardo.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)