 , e seja
, e seja  o subespaço gerado por
o subespaço gerado por
Encontrar uma base e a dimensão de W.
Sempre que é dado um conjunto gerador e quero encontrar uma base de um subespaço de
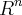 uso um algoritmo dado no livro do seymour lipschutz, que consiste basicamente em escrever os vetores do conjunto gerador como colunas de uma matriz, escalona-la, e daí para cada coluna
uso um algoritmo dado no livro do seymour lipschutz, que consiste basicamente em escrever os vetores do conjunto gerador como colunas de uma matriz, escalona-la, e daí para cada coluna 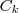 da matriz escalonada que não tiver pivô (primeiro elemento não nulo de uma linha) retirar o vetor
da matriz escalonada que não tiver pivô (primeiro elemento não nulo de uma linha) retirar o vetor 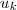 do conjunto gerador. No fim, os vetores que restarem formam uma base do subespaço.
do conjunto gerador. No fim, os vetores que restarem formam uma base do subespaço.Mas nesse caso não estou trabalhando com n-uplas ordenadas, assim não tenho como escrever os elementos desse conjunto gerador como colunas de uma matriz. Como obter uma base para o conjunto em questão? Ou de modo mais geral, como proceder para encontrar uma base de um subespaço de matrizes de ordem n quando é dado um conjunto gerador?


 matrizes
matrizes 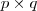 linearmente independentes (L.I.) . Vamos designar o elemento da matriz
linearmente independentes (L.I.) . Vamos designar o elemento da matriz  por
por ![[A_k]_{ij} [A_k]_{ij}](/latexrender/pictures/8934aeb9c7d6bcd8c91ad02f52520059.png) (encontro da i-ésima linha com a j-ésima coluna da matriz A_k) com
(encontro da i-ésima linha com a j-ésima coluna da matriz A_k) com 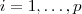 e
e  . Tomemos a combinação linear nula
. Tomemos a combinação linear nula 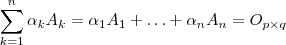 = matriz nula de ordem
= matriz nula de ordem 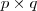 .
.  equações para
equações para  incógnitas .
incógnitas . ![\sum_{k=1}^n \alpha_k [A_k]_{ij} = 0 \sum_{k=1}^n \alpha_k [A_k]_{ij} = 0](/latexrender/pictures/22112e42ba5248e14708ce9fe605ae6c.png) (i=1,...,p ; j=1,...,q)
(i=1,...,p ; j=1,...,q)  em que
em que  é uma matriz
é uma matriz  ;e a cada
;e a cada 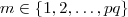 associamos um único vetor
associamos um único vetor ![V_{ij} = ([A_1]_{ij},\hdots , [A_n]_{ij}) \in \mathbb{R}^n V_{ij} = ([A_1]_{ij},\hdots , [A_n]_{ij}) \in \mathbb{R}^n](/latexrender/pictures/9cbe673d4819c38f830fd968c81cdb94.png) que representa sua
que representa sua  -ésima linha .
-ésima linha . 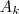 são L.I., então a matriz acima
são L.I., então a matriz acima  e
e  .
. 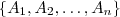 L.I.
L.I. que você postou ,podemos formar por exemplo a seguinte matriz de ordem
que você postou ,podemos formar por exemplo a seguinte matriz de ordem  (a primeira condição já é verdadeira )
(a primeira condição já é verdadeira )  .
.
