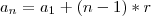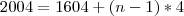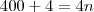por Bernar » Qui Nov 26, 2009 23:19
por Bernar » Qui Nov 26, 2009 23:19
São bissextos todos os anos múltiplos de 4 e não múltiplos de 100;
• Também são bissextos todos os anos múltiplos de 400;
• Não são bissextos todos os demais anos.
Sabendo que o ano de 1600 é bissexto, pode-se afirmar que entre 1601 e 2007 ocorreram:
(A) 97 anos bissextos
(B) 98 anos bissextos
(C) 99 anos bissextos
(D) 100 anos bissextos
(E) 101 anos bissextos
-
Bernar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Set 09, 2009 22:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Sex Nov 27, 2009 13:05
por Molina » Sex Nov 27, 2009 13:05
Bernar escreveu:São bissextos todos os anos múltiplos de 4 e não múltiplos de 100;
• Também são bissextos todos os anos múltiplos de 400;
• Não são bissextos todos os demais anos.
Sabendo que o ano de 1600 é bissexto, pode-se afirmar que entre 1601 e 2007 ocorreram:
(A) 97 anos bissextos
(B) 98 anos bissextos
(C) 99 anos bissextos
(D) 100 anos bissextos
(E) 101 anos bissextos
Boa tarde, Bernar.
Note que essa sequencia de anos que queremos torna-se uma PA, de razão 4. Além disso temos que
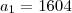
(que é o primeiro ano bissexto no intervalo) e
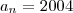
(que é o último ano bissexto no intervalo). Sendo assim:
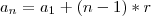
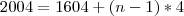

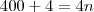

Ou seja, há 101 anos no intervalo que seriam bissextos. Porém, temos que analisar os outros 2 itens:
São bissextos todos os não múltiplos de 100;Nesse caso 1700, 1800, 1900 e 2000 não fariam parte e seriam 'sacados' da nossa contagem, mas pelo outro critério (
Também são bissextos todos os anos múltiplos de 400) temos que o 2000 é bissexto. Sendo assim, só iremos tirar dos 101, três anos.
Resposta: 98.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2584 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Exercício UFG 2009-1
 por wdcardoso » Sex Abr 13, 2012 22:46
por wdcardoso » Sex Abr 13, 2012 22:46
- 5 Respostas
- 3246 Exibições
- Última mensagem por wdcardoso

Sáb Abr 14, 2012 21:12
Geometria Plana
-
- Problema (UNISC 2009)
por Karina » Qui Mar 25, 2010 20:35
- 2 Respostas
- 2560 Exibições
- Última mensagem por Karina

Sáb Mar 27, 2010 13:50
Álgebra Elementar
-
- RACIOCINIO QUANTITATIVO ANPAD 2009
por klein » Dom Ago 22, 2010 17:06
- 1 Respostas
- 4902 Exibições
- Última mensagem por esteban

Seg Nov 01, 2010 14:05
Matemática Financeira
-
- Questão de concurso pmpe 2009 38
por Raphael Feitas10 » Qua Nov 09, 2011 01:24
- 5 Respostas
- 4083 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 14, 2012 21:43
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


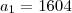 (que é o primeiro ano bissexto no intervalo) e
(que é o primeiro ano bissexto no intervalo) e 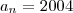 (que é o último ano bissexto no intervalo). Sendo assim:
(que é o último ano bissexto no intervalo). Sendo assim: