 por Pessoa Estranha » Seg Dez 16, 2013 14:27
por Pessoa Estranha » Seg Dez 16, 2013 14:27
Bem, temos 10 filmes disponíveis, dos quais apenas 8 serão transmitidos (2 sessões para cada domingo (2.4 = 8)). Assim, teremos que escolher 8 dos 10 e, por isso, coloquei aqueles 8 tracinhos. Por outro lado, ainda dos 10 filmes, 4 são selecionados para a sessão da tarde, restando 6 para a sessão da noite (6 + 4 = 10). Daí, se quiser, você pode separar aqueles tracinhos em duas partes, uma de 4 e uma de 6, cujos resultados serão multiplicados, conforme o Princípio Fundamental da Contagem. Assim, observe o raciocínio:
1º - (4 tracinhos) - escolhendo 4 filmes entre os 4 disponíveis (os 4 da sessão da tarde):
QUANTOS FILMES TEMOS DISPONÍVEIS PARA OCUPAR O PRIMEIRO TRACINHO, OU SEJA, QUANTOS FILMES, DAQUELES 10, PODEM SER ESCOLHIDOS PARA SEREM TRANSMITIDOS NUM DOS DOMINGOS NA SESSÃO DA TARDE ? (pense e, depois, responda); ESCOLHIDO O FILME DO PRIMEIRO TRACINHO, QUANTOS FILMES PODE-SE SELECIONAR PARA A SEGUNDA SESSÃO DA TARDE, OU SEJA, PARA O SEGUNDO TRACINHO ? (pense e, depois, responda); NOVAMENTE, SEGUINDO O MESMO RACIOCÍNIO, QUANTOS FILMES PODEM SER ESCOLHIDOS PARA O TERCEIRO E QUARTO TRACINHOS ? (pense e, depois, responda). Multiplique, agora, os resultados que você encontrou e reserve.
2º - (6 tracinhos) - escolhendo 6 filmes entre os 6 disponíveis (os 4 da sessão da noite); (sim, 2 filmes estão sobrando):
NOTE QUE 4 JÁ ESTÃO SELECIONADOS PARA A SESSÃO DA TARDE. O QUE QUEREMOS, AGORA, É ESCOLHER 4 DOS 6 DISPONÍVEIS. NOVAMENTE, USANDO OS TRACINHOS, TAMBÉM 4, FAÇO AS PERGUNTAS: QUANTOS FILMES ESTÃO DISPONÍVEIS PARA A TRANSMISSÃO NA SESSÃO DA NOITE DO PRIMEIRO DOMINGO, OU SEJA, DO PRIMEIRO TRACINHO ? (pense e, depois, responda); ESCOLHIDO UM, QUANTOS FILMES RESTAM COMO OPÇÃO PARA A SEGUNDA SESSÃO DA NOITE, SEGUNDO DOMINGO OU SEGUNDO TRACINHO ? (pense e, depois, responda); COM A MESMA IDEIA, QUANTOS FILMES PODE-SE ESCOLHER PARA OS TERCEIRO E QUARTO TRACINHOS ? (pense e, depois, responda); Multiplique, então, os resultados das suas respostas e, novamente, reserve.
Bom, o que você encontrou? Depois, dos resultados obtidos, o que você faria ?


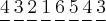 = 8640.
= 8640.
