Tenho um problema e não concordo com a resposta. O problema é: um dispositivo envia mensagens binárias (0,1) para outro dispositivo de forma que o fim de uma transmissão é indicado por uma sequencia de dois bits iguais a 1. Qual é o nº máximo de mensagens distintas que podem ter sido emitidas, sabendo que a transmissão parou ao ser enviado o décimo primeiro bit?
Tenho a resposta como 2 elevado a 11, mas por que, se os dois últimos são iguais a 1?
também?
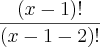... mas como se resolve isso?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)