 por cprado » Qua Dez 11, 2013 11:12
por cprado » Qua Dez 11, 2013 11:12
Boa Noite, Estou com dúvida na seguinte questão, principalmente na potência com expoente decimal negativo... Se alguém puder ajudar agradeço.
(UECE) Se n = (0,5 *

+
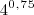
)^2 ?
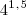
* (1 +
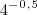
), então
32 * n é igual a:
a) 16
b) 32
c) 48
d) 64
Agradeço desde já.
-
cprado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Dez 11, 2013 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Pessoa Estranha » Qua Dez 11, 2013 17:47
por Pessoa Estranha » Qua Dez 11, 2013 17:47
Olá !
Desculpe, mas a expressão é a seguinte? (É que foi o que eu entendi do que escreveu....).

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por cprado » Qui Dez 12, 2013 13:44
por cprado » Qui Dez 12, 2013 13:44
Isso mesmo,
Obrigado por enquanto.
-
cprado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Dez 11, 2013 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Pessoa Estranha » Qui Dez 12, 2013 16:41
por Pessoa Estranha » Qui Dez 12, 2013 16:41
Bem, para calcular

precisamos, primeiro, calcular o valor de

, dado por

.
Assim, para encontrar tal valor, basta desenvolvermos:

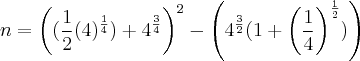
Assim melhorou ?
Tente continuar. Se não conseguir, pode falar ....

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Sex Dez 13, 2013 21:12
por Pessoa Estranha » Sex Dez 13, 2013 21:12
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por cprado » Sex Dez 13, 2013 22:31
por cprado » Sex Dez 13, 2013 22:31
Muito obrigado pela ajuda, estou tentando fazer, mais ainda não cheguei no resultado que é 16. Vou continuar tentando....
-
cprado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Dez 11, 2013 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Pessoa Estranha » Sáb Dez 14, 2013 10:46
por Pessoa Estranha » Sáb Dez 14, 2013 10:46
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por cprado » Sáb Dez 14, 2013 16:44
por cprado » Sáb Dez 14, 2013 16:44
Tudo bem, agradeço pelo empenho... Obrigado!
-
cprado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Dez 11, 2013 10:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Pessoa Estranha » Sáb Dez 14, 2013 18:02
por Pessoa Estranha » Sáb Dez 14, 2013 18:02
Coloque o tópico novamente, quem sabe outro possa ajudar ....
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- expressão com expoente negativo
por Andreza » Dom Jan 08, 2012 15:00
- 1 Respostas
- 2606 Exibições
- Última mensagem por Arkanus Darondra

Dom Jan 08, 2012 15:51
Álgebra Elementar
-
- Derivada de expoente fracionário negativo.
por Sobreira » Sex Out 26, 2012 11:25
- 2 Respostas
- 6306 Exibições
- Última mensagem por Sobreira

Sex Out 26, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
-
- NOTAÇÃO DECIMAL
por laura1970 » Sáb Ago 10, 2013 22:08
- 0 Respostas
- 817 Exibições
- Última mensagem por laura1970

Sáb Ago 10, 2013 22:08
Equações
-
- Número Decimal
por Bielto » Qui Mar 13, 2014 22:59
- 1 Respostas
- 1526 Exibições
- Última mensagem por ant_dii

Sex Mar 14, 2014 03:00
Aritmética
-
- Dúvida elementar de logaritmo decimal
por Fernanda Lauton » Seg Jun 28, 2010 11:18
- 2 Respostas
- 1696 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 28, 2010 14:08
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 +
+ 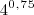 )^2 ?
)^2 ? 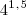 * (1 +
* (1 + 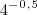 ), então
), então
 +
+ 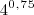 )^2 ?
)^2 ? 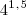 * (1 +
* (1 + 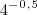 ), então
), então



 precisamos, primeiro, calcular o valor de
precisamos, primeiro, calcular o valor de  , dado por
, dado por  .
.
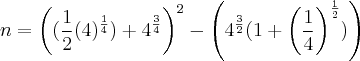


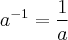
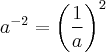
![{a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}} {a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}}](/latexrender/pictures/868408b7067f23f3bb99f23c1e509a3e.png)
![{a}^{\frac{1}{2}} = \sqrt[2]{{a}^{1}} {a}^{\frac{1}{2}} = \sqrt[2]{{a}^{1}}](/latexrender/pictures/64af2824eea82d1b702d96117712bdb0.png)
![{a}^{\frac{1}{2}} = \sqrt[2]{{a}^{1}} = {a}^{0.5} {a}^{\frac{1}{2}} = \sqrt[2]{{a}^{1}} = {a}^{0.5}](/latexrender/pictures/c40edce4674b095d4474ffefc938e5b8.png)


.





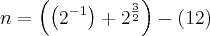
![n = \left(\left({2}^{-1}} \right) + \sqrt[2]{{2}^{3}} \right)-\left(12 \right) n = \left(\left({2}^{-1}} \right) + \sqrt[2]{{2}^{3}} \right)-\left(12 \right)](/latexrender/pictures/49db605f1dd9f9257c2e1a10ed0a5bc7.png)
![n = \left(\left({2}^{-1}} \right) + 4\sqrt[2]{2} \right)-\left(12 \right) n = \left(\left({2}^{-1}} \right) + 4\sqrt[2]{2} \right)-\left(12 \right)](/latexrender/pictures/fcf29f5b36bb7584d34b92a6d50962a9.png)
![n = \left({2}^{-1}} \right) + 4\sqrt[2]{2} -\left(12 \right) n = \left({2}^{-1}} \right) + 4\sqrt[2]{2} -\left(12 \right)](/latexrender/pictures/3ed196917a919840bb8c218ad14bf886.png)
![n = {2}^{-1}} + 4\sqrt[2]{2} -12 \rightarrow n = 4.({2}^{-3} + \sqrt[2]{2} - 3) n = {2}^{-1}} + 4\sqrt[2]{2} -12 \rightarrow n = 4.({2}^{-3} + \sqrt[2]{2} - 3)](/latexrender/pictures/bad0b15d7b1afd1c2d60f454bd0f9502.png)
![n = 4.(\frac{1}{8} + \sqrt[2]{2} - 3) \rightarrow n = \frac{1}{2}+4(\sqrt[2]{2}-3) n = 4.(\frac{1}{8} + \sqrt[2]{2} - 3) \rightarrow n = \frac{1}{2}+4(\sqrt[2]{2}-3)](/latexrender/pictures/2dc386663d08e4a30e0c11affc7ada64.png)
![32n = 32.\left( \frac{1}{2}+4(\sqrt[2]{2}-3) \right) 32n = 32.\left( \frac{1}{2}+4(\sqrt[2]{2}-3) \right)](/latexrender/pictures/a5531be6ed8fbd3faee4eedae777b0ba.png)
![32n = 16+128(\sqrt[2]{2}-3) 32n = 16+128(\sqrt[2]{2}-3)](/latexrender/pictures/262d303e545e2ed024183a9ee5096168.png)
![32n = 16+128\sqrt[2]{2}-384 32n = 16+128\sqrt[2]{2}-384](/latexrender/pictures/2ae828ae16e5f63531051c4862a80ac6.png)













