 por raimundoocjr » Sáb Dez 14, 2013 00:22
por raimundoocjr » Sáb Dez 14, 2013 00:22
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 23 - Pág.: 931)
Utilize coordenadas esféricas.
Calcule
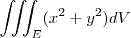
, onde E está entre as esferas x²+y²+z²=4 e x²+y²+z²=9.
Resposta:
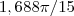
-
raimundoocjr
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral tripla em coordenadas cilíndricas e esféricas
 por karllatorelli » Ter Jul 15, 2014 15:19
por karllatorelli » Ter Jul 15, 2014 15:19
- 0 Respostas
- 1132 Exibições
- Última mensagem por karllatorelli

Ter Jul 15, 2014 15:19
Cálculo: Limites, Derivadas e Integrais
-
- Integral em coordenadas esféricas
 por bruna106 » Sáb Abr 09, 2011 15:22
por bruna106 » Sáb Abr 09, 2011 15:22
- 1 Respostas
- 2712 Exibições
- Última mensagem por LuizAquino

Seg Abr 11, 2011 11:04
Cálculo: Limites, Derivadas e Integrais
-
- [Coordenadas Cilíndricas] Integral Tripla
por raimundoocjr » Sáb Dez 14, 2013 11:07
- 1 Respostas
- 3403 Exibições
- Última mensagem por Russman

Dom Dez 15, 2013 02:55
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de integral tripla com coordenadas polares
por Fernandobertolaccini » Qua Jan 21, 2015 11:05
- 0 Respostas
- 1356 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jan 21, 2015 11:05
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas esféricas
por manuoliveira » Seg Jun 17, 2013 10:18
- 0 Respostas
- 1461 Exibições
- Última mensagem por manuoliveira

Seg Jun 17, 2013 10:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
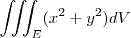 , onde E está entre as esferas x²+y²+z²=4 e x²+y²+z²=9.
, onde E está entre as esferas x²+y²+z²=4 e x²+y²+z²=9.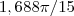

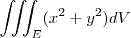 , onde E está entre as esferas x²+y²+z²=4 e x²+y²+z²=9.
, onde E está entre as esferas x²+y²+z²=4 e x²+y²+z²=9.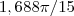

 .
.



