Esse exercício eu não soube nem iniciar.
Se A é um conjunto não vazio então uma operação binária em A é uma função
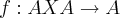 . Qual é o número de operações binárias em um conjunto A com p elementos?
. Qual é o número de operações binárias em um conjunto A com p elementos?a)

b)
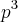
c)
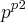
d)
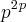
e)
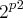
Gabarito: C

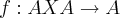 . Qual é o número de operações binárias em um conjunto A com p elementos?
. Qual é o número de operações binárias em um conjunto A com p elementos?
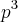
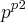
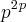
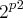

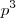 ,de qualquer forma vou postar o que pensei .
,de qualquer forma vou postar o que pensei . 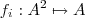 tal que para cada par ordenado em
tal que para cada par ordenado em 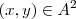 fixado, tem-se
fixado, tem-se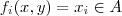 .Como
.Como 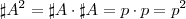 e para cada par ordenado (x,y) é possível definir
e para cada par ordenado (x,y) é possível definir  operações binárias em A ,então ao todo é possível definir
operações binárias em A ,então ao todo é possível definir 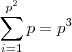 operações binárias em A .
operações binárias em A .
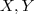 conjuntos com respectivas cardinalidades
conjuntos com respectivas cardinalidades 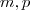 . Defina
. Defina 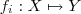 e mostremos que há
e mostremos que há 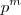 aplicações do conjunto
aplicações do conjunto  ao
ao  .
. 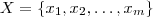 e
e 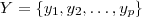 .
. segmentos de retas verticais com as possíveis imagens pela aplicação :
segmentos de retas verticais com as possíveis imagens pela aplicação : (L_1) e chegar em
(L_1) e chegar em  (em L_2) significar que é possível definir uma aplicação tal que
(em L_2) significar que é possível definir uma aplicação tal que  é levado a imagem
é levado a imagem  e
e  é levado a imagem
é levado a imagem  . Uma aplicação ficará bem determinada quando escolhemos um caminho que nos conecta de um ponto de
. Uma aplicação ficará bem determinada quando escolhemos um caminho que nos conecta de um ponto de 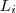 ao outro de
ao outro de 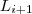 (i=1,... p-1) .
(i=1,... p-1) .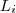 e
e 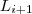 ao longo de
ao longo de 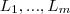 :
: 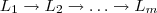
 há
há  formas de chegar em
formas de chegar em  pelo que também há
pelo que também há  maneiras de chegar em
maneiras de chegar em 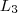 ,..., e o mesmo para chegar em
,..., e o mesmo para chegar em 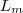 de
de 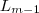 . Por estes esquema há
. Por estes esquema há  (p-vezes) de executar
(p-vezes) de executar 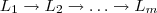 e portanto há
e portanto há 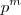 aplicações do conjunto
aplicações do conjunto  ao
ao  .
. 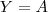 e
e 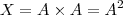 teremos
teremos 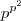 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes