 por Apotema » Seg Nov 23, 2009 14:36
por Apotema » Seg Nov 23, 2009 14:36
tenho sen a=24/25 e sec a negativa, então o valor de
![\sqrt[]{\frac{1-cos a}{1+cos a}} \sqrt[]{\frac{1-cos a}{1+cos a}}](/latexrender/pictures/551e83f69abc7f237b7be8da4e29825a.png)
Pensei o seguinte: sen²+cos²=1
(24/25)²+cos²=1
desenvolvendo a conta:
cos=7/25
substituindo:
![\sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}} \sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}}](/latexrender/pictures/468616a16f39b844966e24636306ad2b.png)
![\sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}} \sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}}](/latexrender/pictures/bb213562112ce9fa2065b84a627709fe.png)
Enfim, não conclui corretamente.
-
Apotema
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Nov 18, 2009 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por thadeu » Qua Nov 25, 2009 15:30
por thadeu » Qua Nov 25, 2009 15:30
Terminando a sua conclusão:
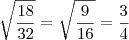
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Apotema » Qua Nov 25, 2009 16:54
por Apotema » Qua Nov 25, 2009 16:54
thadeu escreveu:Terminando a sua conclusão:
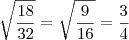
QUE BOBEIRA A MINHA,
-
Apotema
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Nov 18, 2009 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Seno,cosseno,secante, tangente, contangente,conssecante
por leticiapires52 » Seg Ago 11, 2014 14:59
- 4 Respostas
- 2600 Exibições
- Última mensagem por leticiapires52

Ter Ago 19, 2014 13:46
Trigonometria
-
- [Porcentagem negativa.]
por felipel » Sex Jul 25, 2014 11:15
- 0 Respostas
- 3443 Exibições
- Última mensagem por felipel

Sex Jul 25, 2014 11:15
Matemática Financeira
-
- [POTENCIAÇÃO] BASE NEGATIVA
por anneliesero » Seg Jan 28, 2013 15:34
- 1 Respostas
- 1462 Exibições
- Última mensagem por Russman

Seg Jan 28, 2013 18:15
Álgebra Elementar
-
- Radiciação: raíz negativa
por mateushamm » Dom Abr 13, 2014 14:35
- 2 Respostas
- 2924 Exibições
- Última mensagem por Russman

Dom Abr 13, 2014 22:11
Aritmética
-
- Fação impropria negativa, na forma mista
por LuizCarlos » Sáb Mar 17, 2012 02:15
- 5 Respostas
- 3270 Exibições
- Última mensagem por LuizCarlos

Dom Mar 18, 2012 20:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{\frac{1-cos a}{1+cos a}} \sqrt[]{\frac{1-cos a}{1+cos a}}](/latexrender/pictures/551e83f69abc7f237b7be8da4e29825a.png)
![\sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}} \sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}}](/latexrender/pictures/468616a16f39b844966e24636306ad2b.png)
![\sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}} \sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}}](/latexrender/pictures/bb213562112ce9fa2065b84a627709fe.png)

![\sqrt[]{\frac{1-cos a}{1+cos a}} \sqrt[]{\frac{1-cos a}{1+cos a}}](/latexrender/pictures/551e83f69abc7f237b7be8da4e29825a.png)
![\sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}} \sqrt[]{\frac{1-\frac{7}{25}}{1+\frac{7}{25}}}](/latexrender/pictures/468616a16f39b844966e24636306ad2b.png)
![\sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}} \sqrt[]{\frac{18}{25}\frac{25}{32}}=\sqrt[]{\frac{18}{32}}](/latexrender/pictures/bb213562112ce9fa2065b84a627709fe.png)

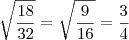



 .
.
 :
: