Então to estudando Equações diferenciais e não entendi uma passagem aqui, estou estudando a parte de variáveis separáveis.
Vejam só.
Notemos que equações do tipo:
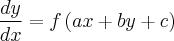 (1.1)
(1.1)Onde a e b são constantes, não são equações de variáveis separáveis, mas podem ser reduzidas a elas por meio da seguinte substituição:
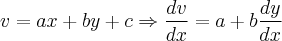 (1.2)
(1.2)Substituindo em (1.1) temos:
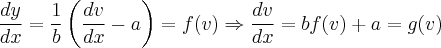
NÃO ENTENDI, o porque de concluir que
 .
.Eu agradeceria se alguém pudesse me ajudar.
Obrigado



 posso afirmar que é igual a isso
posso afirmar que é igual a isso 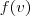 .
.
 ,teremos que
,teremos que 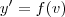 . Mas , derivando-se
. Mas , derivando-se  ,vamos obter
,vamos obter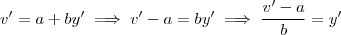 e assim
e assim  .
. 
 .
.
 :
: