INTEGRAL DUPLA - APLICAÇÃO

[sasuyanli]

Olá, gostaria de ajuda no exercício abaixo:

Exercício- D é a região triangular de vértices (0,0), (3,0) e (3,5) e a densidade f em cada ponto 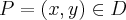é igual à distância de P ao eixo y.

Desenhei a região D, e achei que:




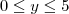
Porém, não consigo encontrar a função f, pois, não entendi essa questão da densidade f em cada ponto ser igual à distância de P ao eixo y.

Se alguém puder ajudar, obrigada.

[e8group]

Acho que você esqueceu que a região D é triangular e considerou a mesma retangular . Note que para cada em tem-se 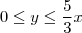e esta é a propriedade do subconjunto do . Então dado em , a menor distância deste ponto ao eixo será .

Agora tente concluir .

[sasuyanli]

Ah, consegui agora.
Muito obrigada!