 por Victor Mello » Ter Nov 19, 2013 21:58
por Victor Mello » Ter Nov 19, 2013 21:58
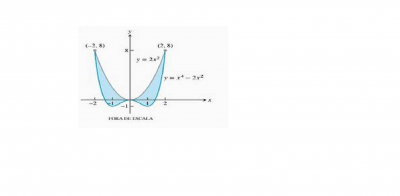
Galera, tentei achar a área dessa curva que deixei em anexo, e eu não consegui encontrar a resposta correta. O gabarito deu 128/15, e eu achei 64/5. Alguém poderia dizer onde ocorreu o erro? Bom, se alguém puder, eu agradeço

Em breve, mais dúvidas sendo postadas.
Obrigado.
- Anexos
-
-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
 por e8group » Ter Nov 19, 2013 23:30
por e8group » Ter Nov 19, 2013 23:30
Analisando parte da região no primeiro quadrante ,podemos calcular esta área por
![\int_{0}^2 2x^2 - [x^4-2x^2] dx \int_{0}^2 2x^2 - [x^4-2x^2] dx](/latexrender/pictures/5d0d74fc31be099fdeab3cce55997f3a.png)
. Determinando o ponto

entre

e

que satisfaz
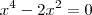
segue que a área da outra parte da região no quarto quadrante pode-se calculada por
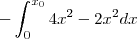
(Sinal negativo pq a área está abaixo do eixo x ). Somando-se estes resultados e por simetria , a área da região será o dobro da soma acima .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Mello » Qua Nov 20, 2013 00:28
por Victor Mello » Qua Nov 20, 2013 00:28
Ahh sim! Parece que agora estou pegando jeito. Eu acho que o meu erro foi por causa da integral negativa, esqueci desse detalhe. Na verdade eu somei as áreas dessas duas curvas sem perceber que a integral negativa indica que está abaixo do eixo x, por isso que deu errado. Valeu pela dica

-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área entre curvas. Sen(x) e x³ em [0, pi]. Alguém ajuda?
por vmoura » Dom Abr 02, 2017 17:56
- 0 Respostas
- 3042 Exibições
- Última mensagem por vmoura

Dom Abr 02, 2017 17:56
Cálculo: Limites, Derivadas e Integrais
-
- Duvida para achar Area entre curvas
por gabrielnandi » Qua Mai 30, 2012 18:23
- 4 Respostas
- 3356 Exibições
- Última mensagem por gabrielnandi

Seg Jun 18, 2012 01:40
Cálculo: Limites, Derivadas e Integrais
-
- Integral, achar a área da região entre as curvas
por Janoca » Sex Jun 06, 2014 17:24
- 5 Respostas
- 4953 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 21:42
Cálculo: Limites, Derivadas e Integrais
-
- [Ajuda]Área de Curvas
por Jhonata » Qua Jun 20, 2012 10:44
- 2 Respostas
- 1683 Exibições
- Última mensagem por Russman

Qua Jun 20, 2012 14:07
Cálculo: Limites, Derivadas e Integrais
-
- Área comum as curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:00
- 0 Respostas
- 1053 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\int_{0}^2 2x^2 - [x^4-2x^2] dx \int_{0}^2 2x^2 - [x^4-2x^2] dx](/latexrender/pictures/5d0d74fc31be099fdeab3cce55997f3a.png) . Determinando o ponto
. Determinando o ponto  entre
entre  e
e  que satisfaz
que satisfaz 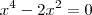 segue que a área da outra parte da região no quarto quadrante pode-se calculada por
segue que a área da outra parte da região no quarto quadrante pode-se calculada por 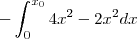 (Sinal negativo pq a área está abaixo do eixo x ). Somando-se estes resultados e por simetria , a área da região será o dobro da soma acima .
(Sinal negativo pq a área está abaixo do eixo x ). Somando-se estes resultados e por simetria , a área da região será o dobro da soma acima .

