 por amanda s » Sáb Nov 16, 2013 09:59
por amanda s » Sáb Nov 16, 2013 09:59
O automovel de seu Julio tem um tanque com capacidade para 45 litros, com esse carro Julio andou 918 km e?
gastou 2 tanques cheios e mais 2/5. Qual é o consumo médio em km/l ?
-
amanda s
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Sex Nov 15, 2013 13:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Sáb Nov 16, 2013 10:43
por nakagumahissao » Sáb Nov 16, 2013 10:43
O consumo médio nada mais é do que a distância total percorrida dividido pela quantidade de litros utilizados neste percurso todo. Dessa maneira, a conta ficaria da seguinte maneira:
A capacidade do tanque é de 45 litros. Gastou no percurso total 2 tanques mais 2/5, logo:

12/5 de um tanque de 45 litros equivalem à:
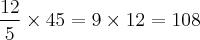
Sabendo-se agora que ele gastou 108 litros de combustível no percurso de 918 km, podemos então calcular o consumo médio:
Consumo Médio = Distância Total Percorrida / Combustível Utilizado = 918 / 108 = 8,5 km/l
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em um calculo de função, ajudem por favor!
por paulohenrique_ » Seg Out 22, 2012 16:29
- 3 Respostas
- 3312 Exibições
- Última mensagem por Russman

Seg Out 22, 2012 18:20
Funções
-
- Calculo sem derivada, me ajudem a resolver por favor
por roberta emiliano » Qua Nov 28, 2012 11:54
- 2 Respostas
- 2584 Exibições
- Última mensagem por roberta emiliano

Qua Nov 28, 2012 14:58
Geometria Analítica
-
- [calculo] ajudem urgente por favor nesse exercicio
por amanda s » Sáb Nov 16, 2013 17:27
- 1 Respostas
- 1999 Exibições
- Última mensagem por nakagumahissao

Dom Nov 17, 2013 10:04
Cálculo: Limites, Derivadas e Integrais
-
- Me ajudem por favor.
por diegodalcol » Qui Mai 22, 2008 13:26
- 4 Respostas
- 4988 Exibições
- Última mensagem por admin

Qui Mai 22, 2008 16:33
Funções
-
- Por favor, ajudem-me!
por hindu » Qua Set 23, 2009 23:08
- 4 Respostas
- 4760 Exibições
- Última mensagem por Lucas Avilez

Ter Out 06, 2009 20:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




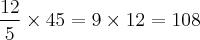



 , avisa que eu resolvo.
, avisa que eu resolvo.

