 por VenomForm » Qui Nov 14, 2013 11:21
por VenomForm » Qui Nov 14, 2013 11:21
Bom primeiramente gostaria de pedir desculpas pois não sei se este é o local certo para minha duvida.
Estou fazendo uma lista de exercícios para estudar quando me deparo com a seguinte questão:
Suponha que você esteja subindo um morro cujo formato é dado pela equação:
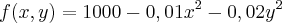
e você esteja no ponto de coordenadas (60;100;764). Em que direção você deve seguir inicialmente de modo a chegar no topo do morro?
Até onde eu sei preciso achar as derivadas parciais de X e de Y e após isto encontrar o vetor gradiente, ai não sei mais o que fazer.
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
 por xGoku » Qua Set 23, 2015 17:19
por xGoku » Qua Set 23, 2015 17:19
Tb não consigo resolver essa... alguém pode ajudar?
-
xGoku
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 23, 2014 21:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por adauto martins » Qui Set 24, 2015 15:38
por adauto martins » Qui Set 24, 2015 15:38
a direçao de maior crescemento de f´(x,y),é dado pela direçao do gradiente,qdo esse tem mesma direçao e sentido de seu vetor unitario,logo:
seja
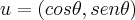
,
![\left|u \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1 \left|u \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1](/latexrender/pictures/4076b0573ee8b6610941b3810525e147.png)
...logo podemos ter:

...
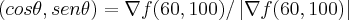
...
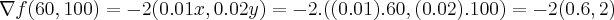
,
![\left|\nabla f(60,100) \right|=\sqrt[]{{(-1.2)}^{2}+{(-4)}^{2}}\simeq 4.18 \left|\nabla f(60,100) \right|=\sqrt[]{{(-1.2)}^{2}+{(-4)}^{2}}\simeq 4.18](/latexrender/pictures/a36f6f097716c4c54266035d54e28ba5.png)
...
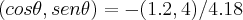
...
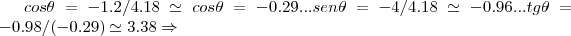
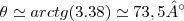
...sera 73.5°N ou 16.5° SD...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Plano tangente e vetor gradiente
por carolzinhag3 » Sáb Abr 15, 2017 23:38
- 0 Respostas
- 1051 Exibições
- Última mensagem por carolzinhag3

Sáb Abr 15, 2017 23:38
Cálculo: Limites, Derivadas e Integrais
-
- [cálculo II] vetor gradiente e derivada direcional
por natanaelskt » Sex Nov 28, 2014 21:09
- 1 Respostas
- 1505 Exibições
- Última mensagem por adauto martins

Sáb Nov 29, 2014 12:13
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo2: Derivada Parcial] Plano tg, Vetor Gradiente
por Claudio Parana » Qua Fev 05, 2014 20:06
- 0 Respostas
- 1202 Exibições
- Última mensagem por Claudio Parana

Qua Fev 05, 2014 20:06
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicações do vetor gradiente] Aplicações das propriedades
 por TheoFerraz » Sex Out 28, 2011 16:14
por TheoFerraz » Sex Out 28, 2011 16:14
- 1 Respostas
- 3318 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:16
Cálculo: Limites, Derivadas e Integrais
-
- [Gradiente - Cálculo 3] Dúvida exercício
por ferfer » Seg Ago 05, 2013 15:54
- 3 Respostas
- 1634 Exibições
- Última mensagem por temujin

Seg Ago 05, 2013 20:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

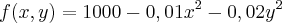


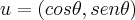 ,
,![\left|u \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1 \left|u \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1](/latexrender/pictures/4076b0573ee8b6610941b3810525e147.png) ...logo podemos ter:
...logo podemos ter: ...
...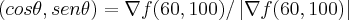 ...
...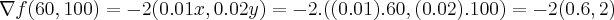 ,
,![\left|\nabla f(60,100) \right|=\sqrt[]{{(-1.2)}^{2}+{(-4)}^{2}}\simeq 4.18 \left|\nabla f(60,100) \right|=\sqrt[]{{(-1.2)}^{2}+{(-4)}^{2}}\simeq 4.18](/latexrender/pictures/a36f6f097716c4c54266035d54e28ba5.png) ...
...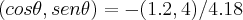 ...
...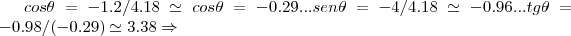
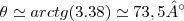 ...sera 73.5°N ou 16.5° SD...
...sera 73.5°N ou 16.5° SD...


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.