 por Victor Mello » Sáb Nov 09, 2013 17:39
por Victor Mello » Sáb Nov 09, 2013 17:39
Alguém poderia me ajudar a resolver esta integral aqui:

Eu fiz por método de integração por partes, chamei cos3x de "u" e
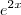
de "dv". Na hora de aplicar a fórmula, o resultado não deu uma integral conhecida. Fiz duas vezes seguidas e ainda não cai um integral conhecida. Bom, espero que tenham me ajudado. =D
Obrigado.
-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
 por e8group » Sáb Nov 09, 2013 18:49
por e8group » Sáb Nov 09, 2013 18:49
Sim é por partes mesmo ,deve aplicar este método duas vezes .
Tome

. Por integração por partes ,temos
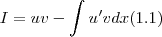
.Se considerarmos

,segue

e


.
Agora tome

para usarmos integração por partes em (1.2) ,
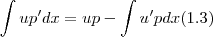
. Notando que

e como já vimos acima
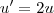
,reescrevemos (1.3) como
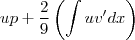
. Só que a expressão entre () é exatamente

.
Se não errei contas é isto .Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Mello » Sáb Nov 09, 2013 19:48
por Victor Mello » Sáb Nov 09, 2013 19:48
Uma dúvida: por que a integral de cos(3x) é sen(3x)/3 e não sen(3x)? Eu vi no formulário que a integral de um cosseno é um seno, estranho...
-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
 por e8group » Sáb Nov 09, 2013 22:25
por e8group » Sáb Nov 09, 2013 22:25
Victor Mello escreveu:Uma dúvida: por que a integral de cos(3x) é sen(3x)/3 e não sen(3x)? Eu vi no formulário que a integral de um cosseno é um seno, estranho...
Por que derivando

chega-se em

. Observe que pela regra da cadeia
![[sin(3x)]' = sin'(3x) \cdot (3x)' = cos(3x) \cdot 3 [sin(3x)]' = sin'(3x) \cdot (3x)' = cos(3x) \cdot 3](/latexrender/pictures/5badf564cafe135d96a450152c63b2b8.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Mello » Dom Nov 10, 2013 14:28
por Victor Mello » Dom Nov 10, 2013 14:28
Ahhh tá, pode crer. Nem tinha percebido que era uma função composta, por isso que não dava certo a integração. Agora fez todo sentido. Obrigado! =D
-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5941 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAÇÃO POR PARTES
por clarivando » Sex Fev 06, 2009 12:03
- 3 Respostas
- 7387 Exibições
- Última mensagem por Marcampucio

Seg Mar 16, 2009 15:50
Cálculo: Limites, Derivadas e Integrais
-
- Integração por partes
por clarivando » Sáb Fev 07, 2009 19:10
- 1 Respostas
- 1987 Exibições
- Última mensagem por clarivando

Ter Fev 10, 2009 20:26
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAÇÃO POR PARTES
por dina ribeiro » Sex Jun 29, 2012 21:23
- 3 Respostas
- 2416 Exibições
- Última mensagem por dina ribeiro

Sáb Jun 30, 2012 13:47
Cálculo: Limites, Derivadas e Integrais
-
- Integração Por Partes
por cardosolrc » Sáb Out 20, 2012 17:28
- 1 Respostas
- 1692 Exibições
- Última mensagem por Russman

Sáb Out 20, 2012 18:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Eu fiz por método de integração por partes, chamei cos3x de "u" e
Eu fiz por método de integração por partes, chamei cos3x de "u" e 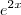 de "dv". Na hora de aplicar a fórmula, o resultado não deu uma integral conhecida. Fiz duas vezes seguidas e ainda não cai um integral conhecida. Bom, espero que tenham me ajudado. =D
de "dv". Na hora de aplicar a fórmula, o resultado não deu uma integral conhecida. Fiz duas vezes seguidas e ainda não cai um integral conhecida. Bom, espero que tenham me ajudado. =D

 . Por integração por partes ,temos
. Por integração por partes ,temos 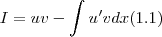 .Se considerarmos
.Se considerarmos  ,segue
,segue  e
e 
 .
.  para usarmos integração por partes em (1.2) ,
para usarmos integração por partes em (1.2) , 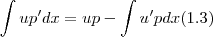 . Notando que
. Notando que  e como já vimos acima
e como já vimos acima 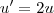 ,reescrevemos (1.3) como
,reescrevemos (1.3) como 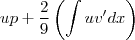 . Só que a expressão entre () é exatamente
. Só que a expressão entre () é exatamente  .
.
 chega-se em
chega-se em  . Observe que pela regra da cadeia
. Observe que pela regra da cadeia ![[sin(3x)]' = sin'(3x) \cdot (3x)' = cos(3x) \cdot 3 [sin(3x)]' = sin'(3x) \cdot (3x)' = cos(3x) \cdot 3](/latexrender/pictures/5badf564cafe135d96a450152c63b2b8.png) .
.




