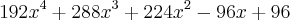por costav13 » Seg Out 28, 2013 11:41
por costav13 » Seg Out 28, 2013 11:41
Dada as Funções f(x) = (2x²+3x-4) e g(x)=(6x²-2) calcule pela regra da cadeia a derivada de f(g(x))+g(f(x))
f ' (g(x)) . g '(x)= 4x+3(6x²)12x
g ' (f(x) . f '(x)= 12x(2x²+3x-4)4x+3
f(g(x))+g(f(x))= 4x+3(6x²)12x + 12x(2x²+3x-4)4x+3
Por favor Alguém pode corrigir pra mim, se esta correta ou se falta alguma coisa, pois só consegui chegar ate ai. Obrigado
-
costav13
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 28, 2013 11:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Taka » Sáb Nov 02, 2013 21:10
por Taka » Sáb Nov 02, 2013 21:10
Não entendi muito bem o que você fez, mas eu tentei resolver essa questão, então segue ai a minha resolução:
Sendo

e
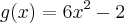
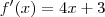
=>


=>

Agora só falta a multiplicação que fica mais simples se você usar o método árabe modificado, que eu particulamente acho muito bom, ou seja, não há colunas diagonais.
O meu resultado deu
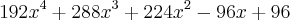
-
Taka
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Nov 02, 2013 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Química
- Andamento: cursando
 por costav13 » Qua Nov 06, 2013 09:37
por costav13 » Qua Nov 06, 2013 09:37
Olá Taka
Em f´(g(x))= 4(6x²-2)= 24x²-8 não seria 4(6x²-2) + 3 = 24x²-8 + 3
Não entedie a multiplicação, tem que multiplicar por quem ?? como vc fez ??
Obrigado.
-
costav13
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 28, 2013 11:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada Corrijam por favor
por costav13 » Seg Out 28, 2013 12:03
- 2 Respostas
- 1684 Exibições
- Última mensagem por costav13

Sáb Nov 02, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Corrijam por favor
por costav13 » Seg Out 28, 2013 18:12
- 1 Respostas
- 1400 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 16:53
Cálculo: Limites, Derivadas e Integrais
-
- [ regra da cadeia ]
por Marimar » Seg Nov 07, 2011 13:34
- 3 Respostas
- 3061 Exibições
- Última mensagem por MarceloFantini

Seg Nov 07, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Regra da Cadeia
por Cleyson007 » Ter Mai 22, 2012 15:17
- 1 Respostas
- 1889 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas- regra da cadeia
por genicleide » Qua Abr 20, 2011 14:28
- 4 Respostas
- 4948 Exibições
- Última mensagem por genicleide

Qua Abr 20, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e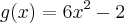
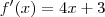 =>
=> 
 =>
=>