 por METEOS » Dom Out 27, 2013 16:59
por METEOS » Dom Out 27, 2013 16:59
Bom dia pessoal,
Estou a precisar de ajuda pois não consigo resolver o seguinte exercício:
"Sabendo que tg ( pi + a ) = -?15 (menos raiz de quinze), e que "a" pertence ]
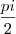
, pi [
Calcule o valor da expressão: cos(-a) + cos (

pi + a) + tg a
Agradecia que me explicassem o porquê de tg (pi +a) dar uma raíz negativa, uma vez que eu achei que tínhamos de reduzir tudo ao 1º quadrante, logo a tangente seria positiva...Não sei se perceberam a minha dúvida, mas qualquer coisa que não percebam digam nas respostas.
-
METEOS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Set 30, 2013 17:04
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciencias
- Andamento: cursando
 por e8group » Dom Out 27, 2013 22:50
por e8group » Dom Out 27, 2013 22:50
Note que se
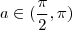
, então

, isto é ,
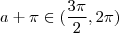
.
Como
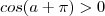
e
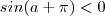
, segue que o quociente

é sempre negativo . Por isso que o número
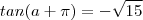
dado é negativo . Certo ?
Para calcular a expressão ,veja a dica :
(1)
![cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi) cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi)](/latexrender/pictures/1562f089af0bdb3e84d842a6ace653e3.png)
(2)
![cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a) cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a)](/latexrender/pictures/2cdff3bd07f457189e0f9c0a681fd800.png)
.
...
Consegue terminar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por METEOS » Seg Out 28, 2013 17:17
por METEOS » Seg Out 28, 2013 17:17
Então, em que casos é que devemos efectuar uma redução ao 1º quadrante? Poderíamos efectuar neste caso uma redução ao 1º quadrante?
-
METEOS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Set 30, 2013 17:04
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciencias
- Andamento: cursando
 por e8group » Seg Out 28, 2013 18:14
por e8group » Seg Out 28, 2013 18:14
Para qualquer arco

pertencendo ao primeiro ,segundo ,terceiro ou quarto quadrante ,podemos reduzir o mesmo em relação ao primeiro quadrante.
Mas foi dado que tan(a+\pi) = - \sqrt{15} [/tex] e o arco

pertence ao quarto quadrante ,como vimos no post acima . O arco

pertence

,isto é , ele está no segundo quadrante .Sendo assim seria desnecessário reduzir a+\pi ao 1° quadrante .
Observe que a soma dada se reduz a
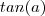
.Qual a relação entre
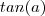
e
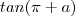
?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por METEOS » Seg Out 28, 2013 18:27
por METEOS » Seg Out 28, 2013 18:27
"Qual a relação entre tan(a) e tan(\pi + a) ?"
Caso a seja do 2º quadrante, e pi+a pertença ao 4º quadrante.
No caso de a seja do 1º quadrante, e pi+a seja do 3º quadrante, também são iguais
Elas são iguais certo?
-
METEOS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Set 30, 2013 17:04
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciencias
- Andamento: cursando
 por e8group » Seg Out 28, 2013 19:05
por e8group » Seg Out 28, 2013 19:05
Sim .

. A função tangente é periódica de período

, logo para quaisquer que seja

(com k inteiro ) teremos a igualdade
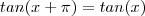
.Pode-se confirma esta igualdade utilizando a fórmula de adição de arcos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressoes
por Biinha » Ter Fev 19, 2013 16:55
- 4 Respostas
- 2433 Exibições
- Última mensagem por Biinha

Sex Fev 22, 2013 11:41
Conjuntos
-
- expressoes
 por Bernardo Silva » Sáb Nov 19, 2016 16:40
por Bernardo Silva » Sáb Nov 19, 2016 16:40
- 1 Respostas
- 1619 Exibições
- Última mensagem por Jadiel Carlos

Seg Nov 21, 2016 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [expressões] ajuda
por kaic » Seg Abr 07, 2008 23:48
- 5 Respostas
- 3967 Exibições
- Última mensagem por admin

Ter Abr 08, 2008 05:04
Álgebra Elementar
-
- [expressões] problema
por Cleyson007 » Ter Jul 01, 2008 01:43
- 9 Respostas
- 16487 Exibições
- Última mensagem por paulo testoni

Qua Out 01, 2008 16:23
Álgebra Elementar
-
- Cálculo de Expressões
por Jansen » Dom Ago 30, 2009 01:28
- 2 Respostas
- 2811 Exibições
- Última mensagem por Jansen

Dom Ago 30, 2009 17:17
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
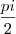 , pi [
, pi [ pi + a) + tg a
pi + a) + tg a

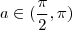 , então
, então  , isto é ,
, isto é , 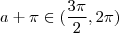 .
. 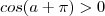 e
e 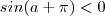 , segue que o quociente
, segue que o quociente  é sempre negativo . Por isso que o número
é sempre negativo . Por isso que o número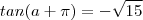 dado é negativo . Certo ?
dado é negativo . Certo ?![cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi) cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi)](/latexrender/pictures/1562f089af0bdb3e84d842a6ace653e3.png)
![cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a) cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a)](/latexrender/pictures/2cdff3bd07f457189e0f9c0a681fd800.png) .
. 
 pertencendo ao primeiro ,segundo ,terceiro ou quarto quadrante ,podemos reduzir o mesmo em relação ao primeiro quadrante.
pertencendo ao primeiro ,segundo ,terceiro ou quarto quadrante ,podemos reduzir o mesmo em relação ao primeiro quadrante. pertence ao quarto quadrante ,como vimos no post acima . O arco
pertence ao quarto quadrante ,como vimos no post acima . O arco  pertence
pertence  ,isto é , ele está no segundo quadrante .Sendo assim seria desnecessário reduzir a+\pi ao 1° quadrante .
,isto é , ele está no segundo quadrante .Sendo assim seria desnecessário reduzir a+\pi ao 1° quadrante . 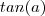 .Qual a relação entre
.Qual a relação entre 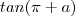 ?
? . A função tangente é periódica de período
. A função tangente é periódica de período  , logo para quaisquer que seja
, logo para quaisquer que seja  (com k inteiro ) teremos a igualdade
(com k inteiro ) teremos a igualdade 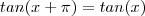 .Pode-se confirma esta igualdade utilizando a fórmula de adição de arcos .
.Pode-se confirma esta igualdade utilizando a fórmula de adição de arcos .

 , avisa que eu resolvo.
, avisa que eu resolvo.

