Ando aqui às voltas com este exercício e não consigo resolver o mesmo, será que me podem dar uma maozinha?
Considere o círculo trigonométrico representado no referencial o.n. Oxy da figura (da imagem), ao qual pertencem os pontos P e Q. Seja alfa a amplitude do ângulo POR e R o ponto de intersecção da semirecta OQ com a recta r, paralela ao eixo Oy e que intersecta o eixo Ox em P. Considere ainda o arco RS, centrado em P. A abcissa do ponto S em função de alfa é:
a) cos alfa - tg alfa b) 1+ tg alfa c) sen alfa - tg alfa d) 1-tg alfa
Uploaded with ImageShack.us
Obrigada
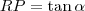
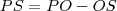
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)